期中考试就要到了，今天复习了高数，对梯度这一概念产生了疑惑，因为平常上课爱打瞌睡，对很多概念自然很不到位，查了一些资料，才明白大体的意思。

什么是梯度？

梯度的计算结果会是”在每个位置都算出一个向量,而这个向量的方向会是在任何一点上从其周围标量值最小处指向周围标量值最大处.而这个向量的大小会是上面所说的那个最小与最大的差距程度”

简单地说，梯度指向的就是在函数某一点变化最大的反方向。梯度就是这样定义的，所以别问为什么梯度就是函数在某一点处最大变化反方向。我们给“函数在某一点处最大变化反方向”取个外号，就叫“梯度”。

来举一个已经用烂了的栗子：

假如你在一座山上，怎样用最短的距离到达山谷中最低点的湖泊？

这时，梯度就开始发挥了作用。

我们只需要照着等高线，朝着梯度最大的方向，一直沿着梯度相反的方向就可以到达谷底（原理和弹珠从高处滚落最后会滚进最低处一样）。

为什么梯度反方向就是函数在某一点处最大变化方向？

梯度与方向导数密不可分

设 $u = f(x,y,z)$，有一点$P(x,y,z)$

对于一个特定的方向l，$\frac{\partial u}{\partial l}$就是点P在方向l上的方向导数。

$\frac{\partial u}{\partial l} = \frac{\partial u}{\partial x}·cosα +\frac{\partial u}{\partial y}·cosβ +\frac{\partial u}{\partial z}·cosγ$

其中，α、β、γ是l的方向余弦。

我们把这个式子向量化，有

$\frac{\partial u}{\partial l} = (\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z})·(cosα,cosβ,cosγ)$

使

$A = (\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z})$

$B = (cosα,cosβ,cosγ)$

则

$\frac{\partial u}{\partial l} = A · B$

所以

$|\frac{\partial u}{\partial l}| = |A||B|cosφ$

我们都知道，$\frac{\partial u}{\partial l}$表示的是点P在l方向上的变化率

变化率要想最大，就一定要使$cosα=1$。

巧合地，当$cosα=1$，A的反方向恰好就是最大的变化方向。

好了，现在我们已经找到函数值下降最快的方向了，这个方向就是和向量相同的方向.那么此时我把A向量命名为梯度（当一个点确定后，梯度方向是确定的），也就是说明了为什么梯度反方向是函数变化率最大的方向了。

联想

上个学期在学习机器学习的线性回归的时候，接触到了梯度下降算法，当时不明白是什么意思，也没有深究，如今才逐渐明了。

在线性回归中，我们假设了一个函数，称其为假设函数(hypothesis function)，使用某些很厉害的步骤来训练假设函数。

在监督学习中，为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本（xi,yi）(i=1,2,…m)
（xi,yi）(i=1,…),采用线性回归，损失函数为：

$J(θ0,θ1)=\sum_1^m{(hθ(xi)−yi)^2}$

而使用梯度下降(Gradient Descent)，就可以求得最优解（实际上有可能不是最优= =）

梯度下降：

update = learning_rate * gradient_of_parameters

parameters = parameters - update
(懒得打公式了= =)

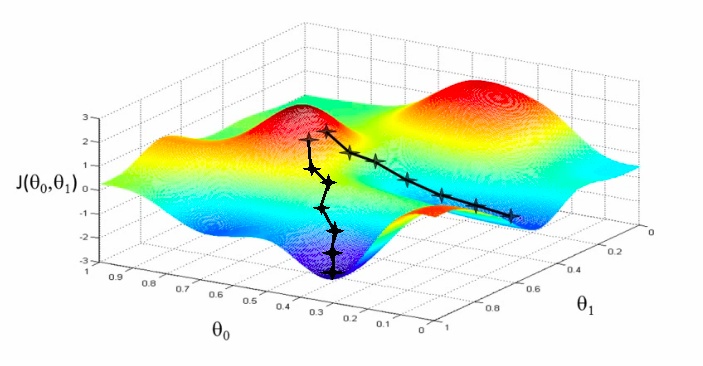
其实线性回归也好，逻辑回归也好，其本质就是拟合，梯度下降算法将其CostFunction减到最小，就像从山顶爬到山谷一样（见文首的图），但直观上看，山谷又不只有一个，如果有好几个山谷，山谷有深也有浅，我们可没有办法选择是到哪一个山谷，这个时候就出问题了。

然后又出现很多弥补这个缺点算法啦，比如说 随机梯度下降(Stochastic gradient descent)、小批量梯度下降(Mini-batch gradient descent)之类的，还有牛顿法、涅斯捷罗夫梯度加速(Nesterov accelerated gradient)balabala的，我也不懂，就不说了。

赏

谢谢你请我吃糖果

支付宝

微信