第三章 模块化、对象和状态

Mεταβάλλον ὰναπαύεταιw
(Even while it changes, it stands still.) —Heraclitus
Plus ça change, plus c’est la même chose. —Alphonse Karr

上一章实际上叙述了基于被模拟结构去设计程序的结构，而这一章将阐释两种不同策略：一种重点在于对象，另一重在于信息流。两种策略将使我们抛弃老的代换模型，转向新的环境模型。同时，因为时间成了最大的问题，所以还会引入并行概念。

赋值和局部状态

局部状态变量

我们以银行账户系统为例，为了实现一个可以实现取钱和存钱的银行账户，我们可以这样设计：

其中使用了特殊形式set！，其语法是：
(set! )
意即将赋值给这个变量。
以上的程序设计有问题，因为balance是全局变量，任何过程都能访问到balance，所以我们就需要局部变量：

我们可以运用第二章学到的信息传递风格，完善我们的程序：

这样的设计方法非常精妙，值得再三品味。

赋值的优缺点

到此，我产生了以下疑问：什么叫赋值？
简单地说，赋值就是 set! 操作，动态地改变某一变量索引的值。

接下来我们会看到赋值具有缺陷，但其优点也是显而易见的，在很多问题上，善用赋值会帮助我们加强程序的模块化。下面以rand过程的设计为例：
我们计划通过rand生成一系列符合均匀分布的随机数，

我们当然可以不用赋值，直接rand-update操作即可，但这会带来很大复杂度，我们以蒙特卡洛仿真为例：
我们知道，6/π^2是随机选取两个整数之间没有公因数子的概率，我们利用这个事实进行大量实验，最后就能得出π的近似值。
具体代码不在这写出，我只讨论需要用到生成随机数的部分。在对大量随机数的选取步骤中，采用赋值方式的rand，我只需要使用两次rand即可，而如果使用rand-uodate，我就需要显式地操作let ((x1 (rand-update x)))和let ((x2 (rand-update x1))))，这将会十分麻烦。

目前我们可能这样总结：运用赋值的方式，将会把哪些原本需要显式操作的过程封装起来，使程序更加模块化。但事实并非如此。

只要不用赋值，以同样参数对同样过程的两次求值，结果一定是相同的，所以可以认为我们在计算函数。就像我们在前两章所做的那样，不用任何赋值的程序设计称为函数式程序设计。

我又产生了这个疑问：let与set!有什么区别？
let是lambda表达式的语法糖，即：(let ((var val) …) exp1 exp2 …)，为 ((lambda (var …) exp1 exp2) val …)。一句话，let就是lambda。而set!是赋值操作。

注：在scheme中，类似于set!，结尾加“！”是scheme的一种命名约定，表示改变变量的值。

在赋值下，无法使用代换模型。而代换模型的本质就是，一个符号其实只是一个值的的名字或者说是代号。但赋值则将一个变量变成了储存着可变数值的位置，可以说，变量与数值分离了。

函数式编程的内部是静态的，而命令式编程（即广泛运用赋值的程序设计）则是动态的，一旦将变化引入程序设计，就会混淆很多函数式编程中简洁明了的概念。

在函数式编程中，任何被定义的对象都是一个过程。举个例子，我定义w1、w2为运用函数式程序设计思维设计的银行账户，因为这个银行账户过程内部是静态的，故相当于将这个处理余额的过程传递给w1、w2，所以在本质上，w1和w2是一回事，它们都代表着一个函数，一个过程。

而在命令式编程中，任何被定义的对象都是完全不同的东西。仍然拿银行账户为例，这个银行账户用命令式程序设计思维设计，同样定义w1和w2为两个银行账户，则两者就是截然不同的东西了，w1的操作与w2的无关，两者不能互相替代。

在运用赋值之后，通过等价替换去简化表达式的问题就变得异常复杂，对其推理也变得十分困难。

广泛采用赋值的命令式程序设计不仅会存在解释性困难的问题，还会出现额外的逻辑问题。以求阶乘为例：
这是函数式的风格：

这是命令式的风格：

如果我们对两个赋值操作改变顺序，就会出现错误，这个错误显而易见，不多解释。而这种错误绝对不会出现在函数式程序设计中。所以，在命令式程序设计中，需要我们额外思考赋值顺序带来的问题。

在生活中，从物理的角度看，每个独立对象都由数种独立状态组成，我和你有相同的独立状态名称：身高、体重、血压、心率……那么。我们该如何确定两个对象之间的独立性呢？举个例子，假设我们有两只粉笔，而这两只粉笔的所有独立状态参数都是一样的，比如说长度、表面粗糙度、重量等等，那么我们如何去区分这两只粉笔就是两个独立个体，而不是一支粉笔和其在镜子前的投影呢？答案就是改变，我把一支粉笔折了，如果另一只粉笔没有变化，那么就可以确定两支粉笔是独立的。但是，问题又来了，我现在拿出指甲钳剪下自己的一小片指甲，现在的我改变了，而一秒前的我没改变，那按理说我不该是我，或者换句话说，我无法判断我就是我，而赋值和对象的使用，则为程序设计引入了这样的哲学问题。

求值的环境模型

术语：
约束
约束变量（bound variables）
自由变量（free variables）
作用域（scope）
lambda表达式是约束变量的唯一方式，它是唯一能创建名字的东西。Define可以被避免。

两个规则

环境模型，本质上来说，是由一串由指针连接至父环境的序列。define操作将定义的对象固定在父环境中，这个对象指向形参和一串描述操作过程的代码。举个例子，假设我有以下操作：

那么他们在环境模型中的表示就为：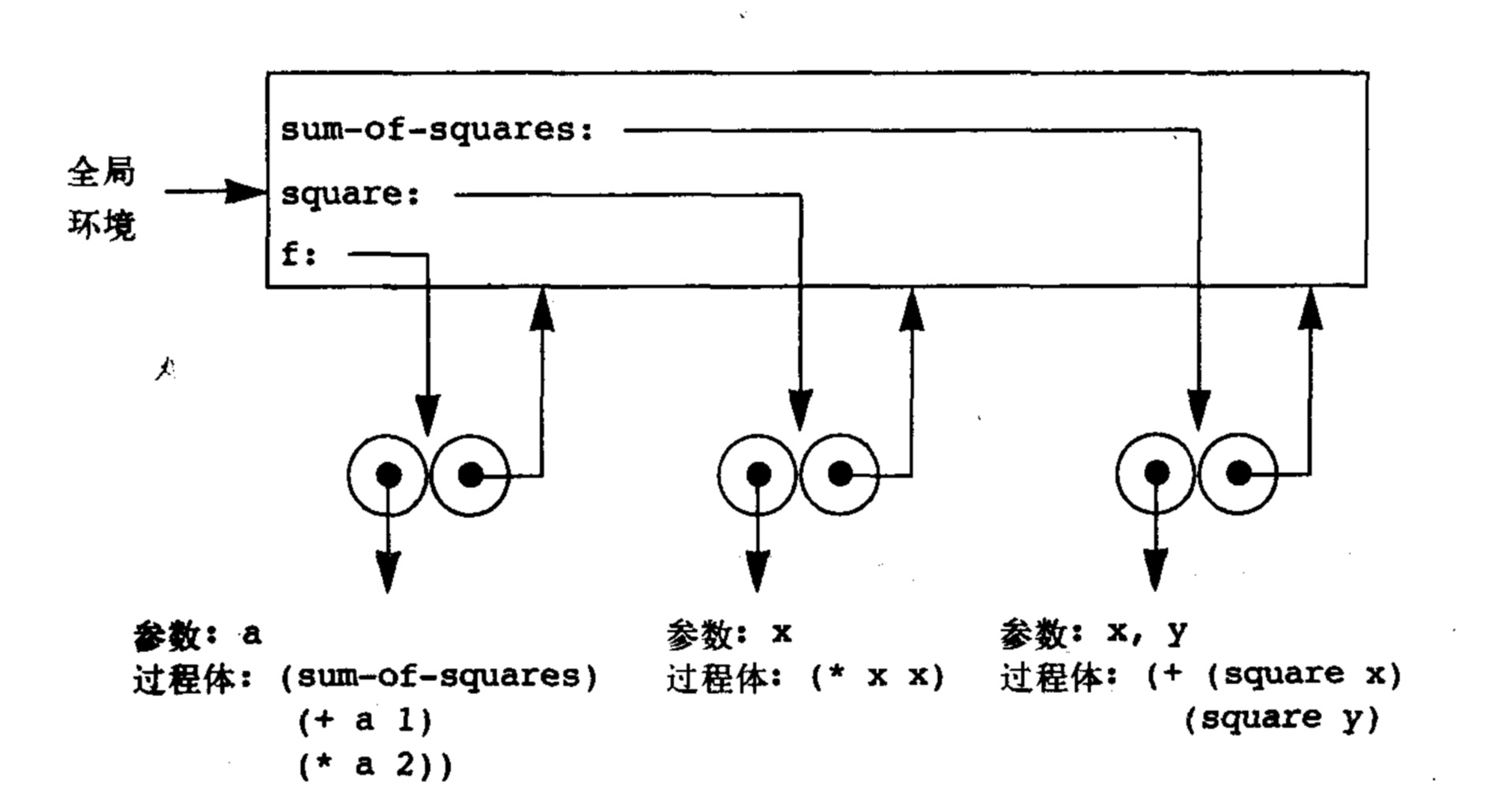

在调用这些过程进行具体的数值运算时，我们需要创建一个新的子环境来储存参数的值，这个子环境指向父环境，获取过程的具体实现代码，创建一个将参数代入的具体过程，并将这个过程结果返回至上一级环境。

再举一个更通俗的例子，我设计了一个计数器：

1
2
3
4
5

(define make-counter
    (lambda(n)
        lambda()
            (set! n (+ 1 n))
            n))

1
2

(define c1 (make-counter 0))
(define c2 (make-counter 10))

1
2

(c1)
(c2)

用变动数据做模拟

静态的数据抽象：构造函数、选择函数<——>动态的数据抽象：2 + 改变函数

表结构

数据与对象<——>同一和共享

考虑

1
2

(define x (list 'a 'b))
(define z1 (cons x x))

与

1

(define z2 (cons (list 'a 'b) (list 'a 'b)))

的区别，z1是共享，而z2是同一，前者是对象，后者是数据。两者的结果是一样的，但进行数值变化后，会有不一样的结果。

所以

1

(eq! (car z2) (cdr z2))

的结果是FALSE，而

1

(eq! (car z1) (cdr z1))

的结果是TRUE，这是因为(eq! x y)其实在检查x和y是否是同一个对象，而不是检查其内容是否相等。

改变即是赋值

我们对序对可以这样构造

我们可以将赋值内嵌在序对的构造函数中

精妙的cons

下面看一个由丘奇(Alonzo Church)定义的cons、car、cdr，

用lambda表达式定义的，不依赖于任何操作的完美的序对，太精妙了。

1
2
3
4
5
6

(define (cons x y)
    (lambda(m)(m x y)))
(define (car x)
    (x (lambda(a d) a)))
(define (cdr x)
    (x (lambda(a d) d)))

太美了。

队列

根据数据抽象，我们可以将构造一个队列分离成三个部分：

*构造函数

1

(make-queue)//创造一个空的队列

*选择函数

1
2

(empty-queue? <queue>)
(front-queue <queue>)//返回对列头对象

*改变函数

1
2

(insert-queue! <queue> <item>)
(delete-queue! <queue>)

高效插入和删除数据的结构：

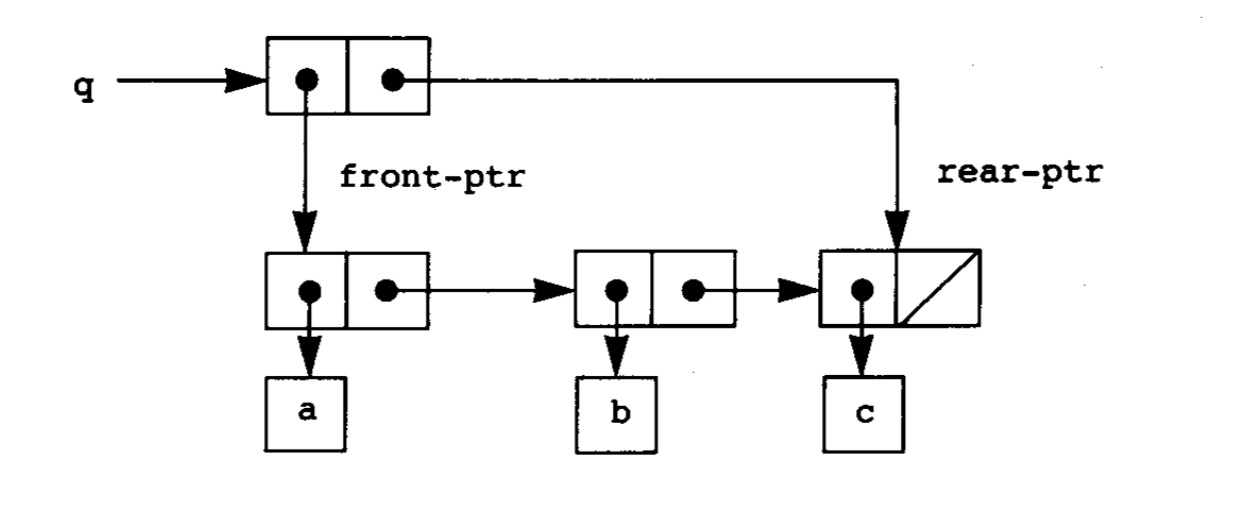
如此一来我们只需要索引表的两个头，就能索引整个队列。

过程的具体实现：

**

表格

之前我们运用表格的方法实现了数据导向式的程序设计，通过两个关键词索引指向的过程，这次我们要设计一个基于表的可变动的表格。

一维表格

首先考虑一维表格，每个记录包括一个关键词和对应的值，所以我们可以用一个序对表示，那么很自然的，可以想到下面的结构：

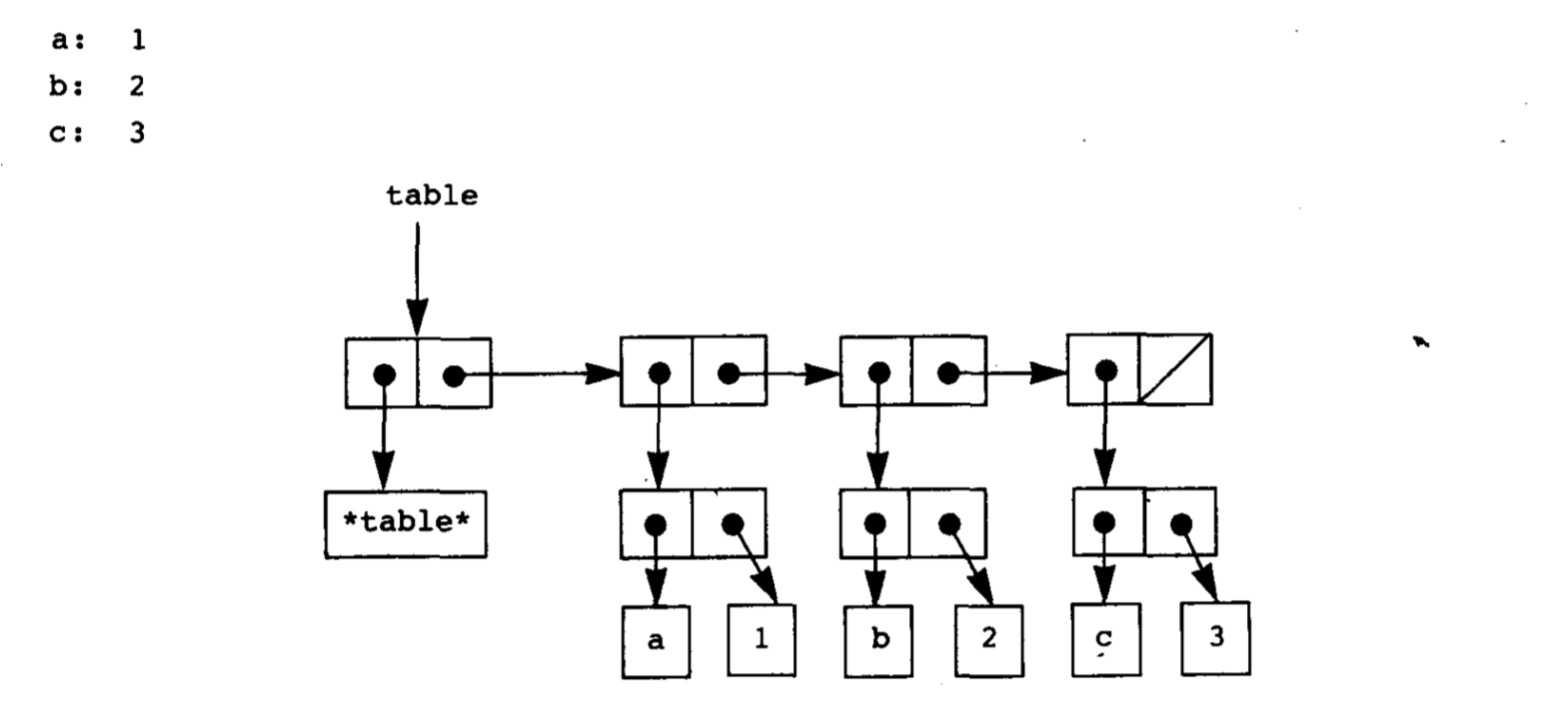
其中，为了能够增加记录，我们需要将表序列的表头标记为“表头”，图中为*table*。

为了查找是否存在参数，我们需要定义一个查找函数lookup。

为了插入一个记录，我们同样需要定义一个插入函数insert!

二维表格

二维表格的构造是基于一维表格的，直观上说，就是一维表格的延伸，在一维表格的第一个索引处建立另一个一维表格，结构如图：

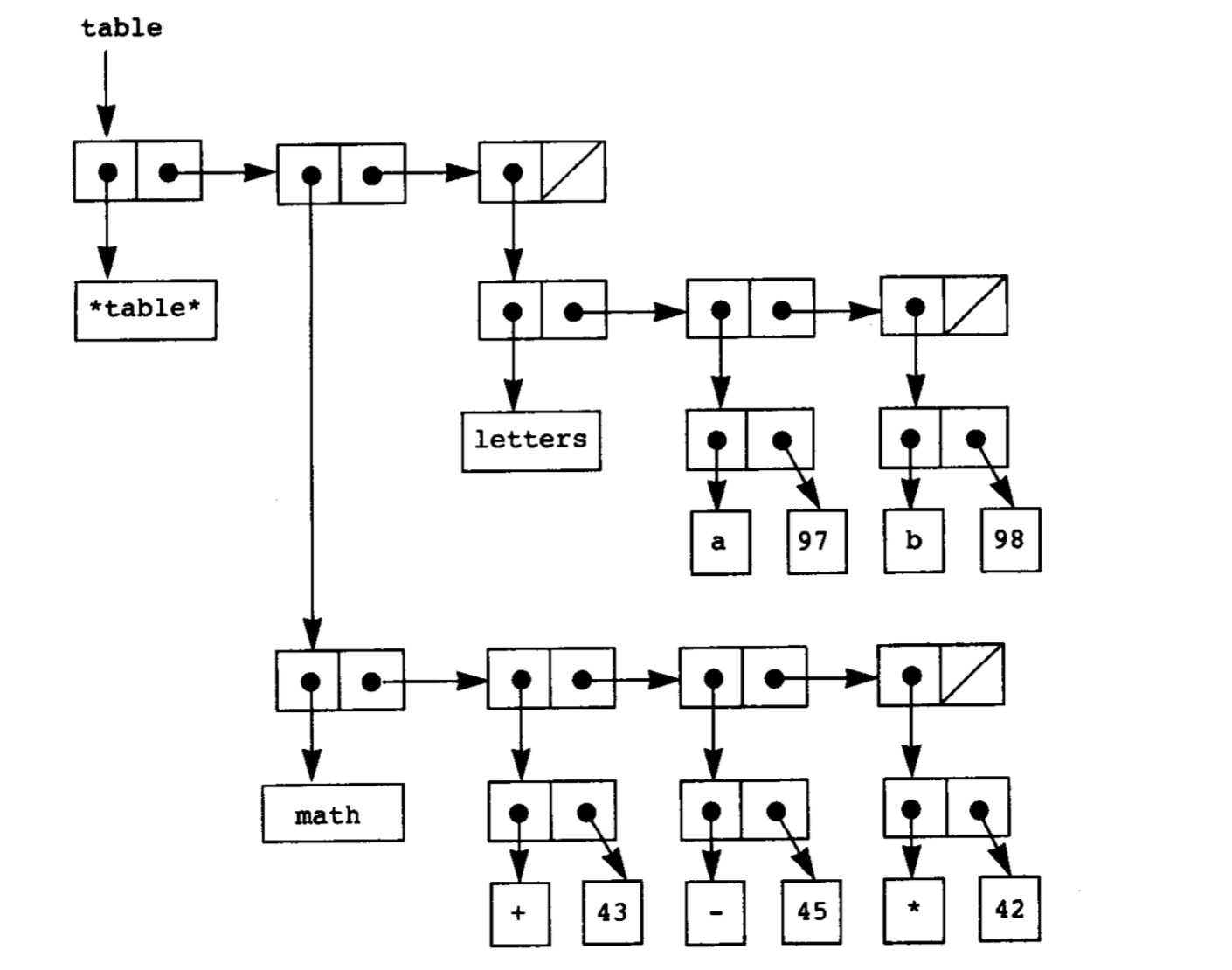
其查看函数、插入函数就是基于一维表格两个函数的嵌套。

约束系统

就拿 $F=ma$ 这个公式来说，力、质量和加速度之间的关系不是单向的，而是循环的，我只要知道了其中的两个，就能求解出第三个。但依照之前的计算机程序设计思维，我们必须要显式地设计求特定值的程序，即必须确定输入输出。求F的程序只能求F，求m的程序只能求m。而这一节就要介绍一种使程序不再是单一的input——>output，简单来说能够描述变量间关系的方法，即约束系统。老样子，我们先看结论再分析。

下面是一个用约束网络表示的$9C=5(F-32)$，华氏度与摄氏度转换的公式：

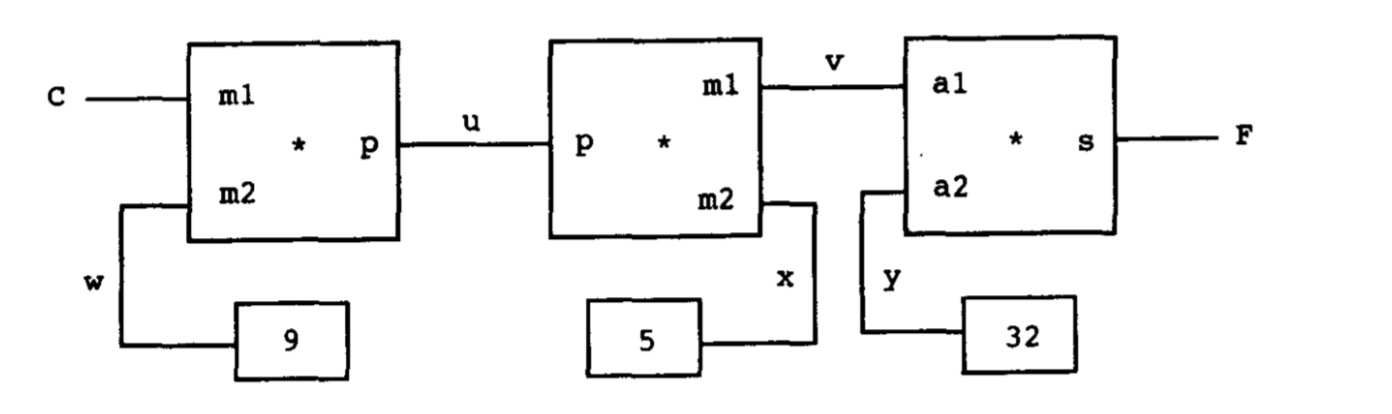
我们的想法是，当其中某个模块被赋值激活，它就会去唤醒与之相连的约束，进而去唤醒与之相连的其他模块，如果前一个模块包含的信息能够确认与之相关的模块的值，那么该模块就被前一个模块激活，以此类推。有点像神经元之间的信号传递，也有种追溯的感觉。

约束系统还要仔细看看P201~

并发

赋值将 时间 带进程序设计

并发将程序对现实世界的模拟更进一步、更加模块化、速度更加快

并发的问题与约束

尚未规范的并发会导致的问题：

对并发程序的限制：1.严格禁止；2.结果对照；3.也可以不限制，具体情况具体分析

控制并发的机制

串行化组：将不相关的进程都放在一起，形成一个个串行化组，组内的进程不能同时运行，不同组可以同时运行。

流

我们对赋值的引入，目的在于将程序更加模块化。由于程序实际上是对现实事物的模拟，我们试图将程序分成和组成现实事物一样的小部分、子系统，来实现更加优秀的模拟。但赋值的引入也会带来很多问题，我们不能更加数学化的编写和分析程序，而会去在意更多思想外的东西。但如果我们对这个世界的认识就是错误的呢？或者说，我们对事物的组成就是错误的呢？我们的看法错误，根据这个看法对程序进行模块化的改变，自然就是错误的。那么我们能否从另一个角度分析一个问题呢？

流处理避免赋值的同时实现状态的模拟，这样做避开了由赋值带来的弊端。流处理的好处是，建立了一个约定的接口，将每个过程可以作为一个公用的模块去任意构建程序。

表与流的区别

delay、force

流基本操作的表示

记忆化（对delay的改造）

无穷流

表示正整数

厄拉多塞筛法

隐式定义流：整数和斐波那契数

流计算模式的使用

序列加速器

赏

谢谢你请我吃糖果

支付宝

微信