
王阳学长和我说《线性代数的本质》和《微积分的本质》这两个系列的视频对理解两个学科有很大帮助,我最近才刚刚看完= =效率还是很低的。
微积分在半个月前(左右)看完了,那时候还没有想到把笔记记录下来,看线性代数的时候算是想到了,就写了写,而且这些也不是完整的,只是零碎的我觉得受益匪浅的内容。
线性变换在矩阵中的表示
线性变换的条件
变换后的坐标轴网格平行且等距
每一个向量都是由其基向量来表示的
因此,只要知道基向量的坐标变换,就能得出线性变换后的所有向量的坐标。
基于以上想法,我们有以下求线性变换的方法:
e.g a = 1i + 2j;线性变换后,a‘ = 1i’ + 2j’;只需要知道i‘是多少,j’是多少,就可以了。
用矩阵乘法表示:
(a,c)和(b,d)表示的是基向量i、j在线性变换后的坐标。
(x,y)是我们要求的向量,在举的例子中,相当于(1,2)。
行列式的意义
设行列式等于n。行列式表示线性变换后,单位面积(体积)的图形被扩大(缩小)了n倍。换句话说,行列式的数值等于由n个向量围成的n维空间物体的某个东西(二维是面积,三维是体积,四维是什么?五维是什么?……)
叉乘
三个向量的行列式等于平行六面体的体积。三个向量的行列式可表示为两个向量的点积:点积表示的是一个向量的投影乘以另一个向量,而行列式表示的是两个向量围成的面积乘以高,而这个高就是第三个向量在两个向量公法向量上的投影。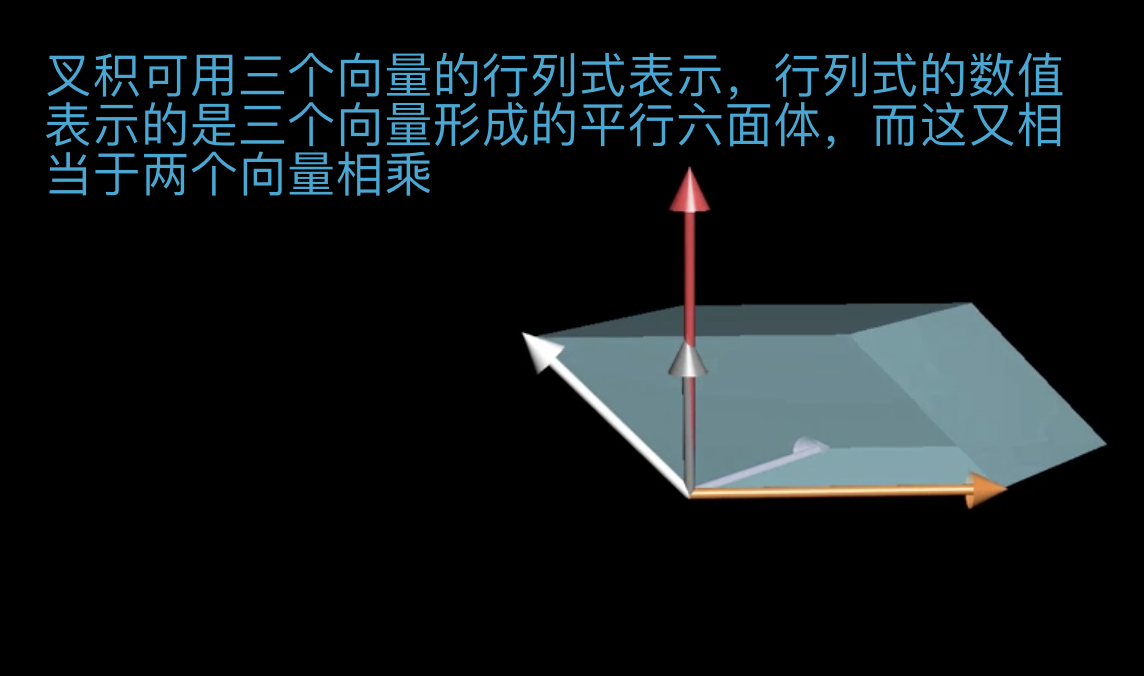
基变换
矩阵的表示是基于基向量的选择的,但基向量并没有规定就是我们通常使用的直角坐标系。 那么如何转化不同基向量,或者说,如何把在一个基向量系中的线性变化 转换为另一个基向量系中的表示呢?
特征向量与特征值:
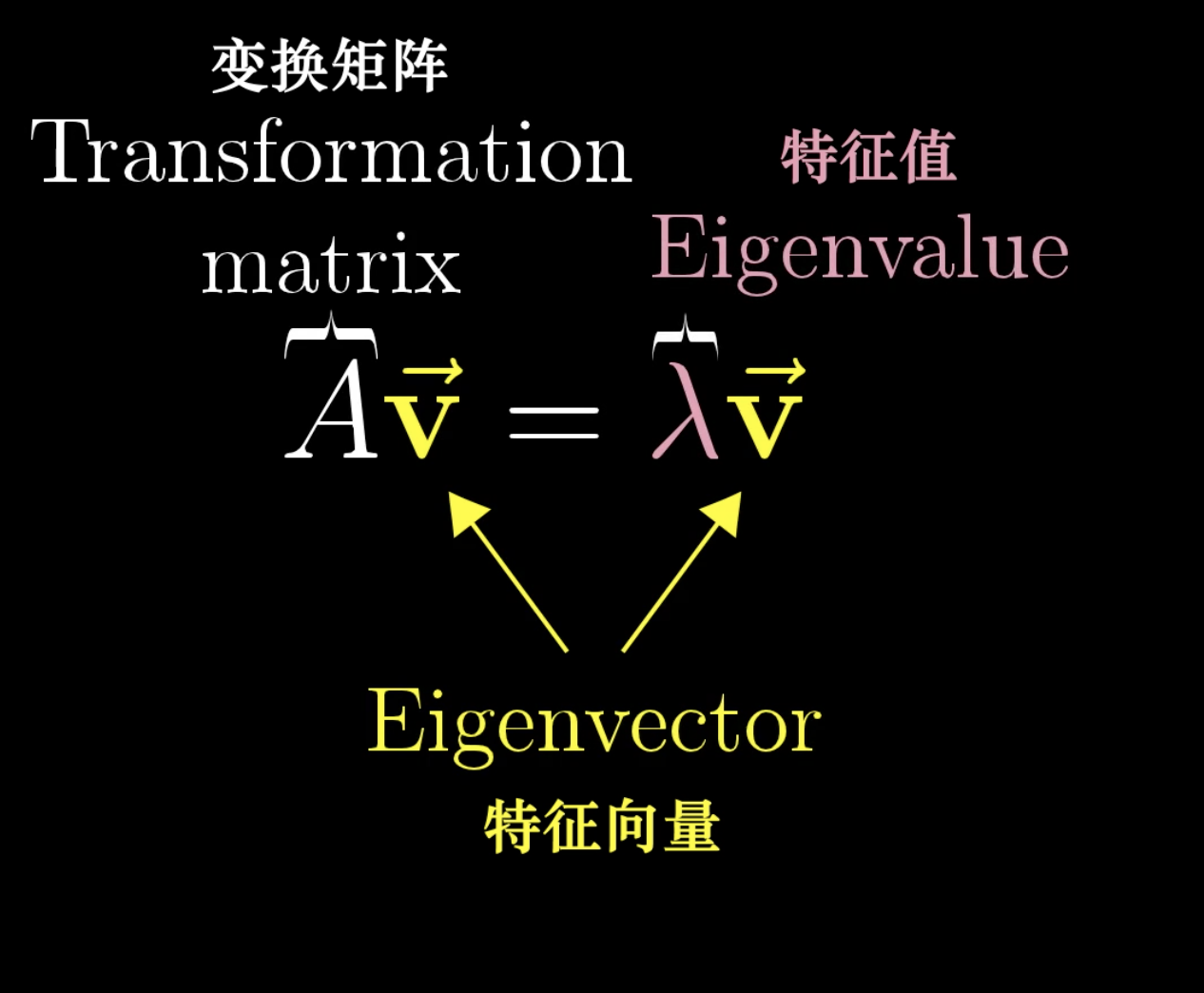
AX = (lambda)X
这是特征向量和特征值的计算公式
这个公式有什么几何意义呢?
我们知道,矩阵相乘,表示的是线性变换,所以,这个式子的意思是,X向量经过线性变换后,并没有旋转,而是在它所张成的空间中扩张或缩小。有这种性质的X,就叫做特征向量,lambda,就是X在线性变换后的扩张缩小的系数,叫做特征值。
那么特征向量有什么意义呢?
因为特征向量只是在其张成的空间中变化,所以对于一个线性变化的体,其变化其实就是以其特征值为一的特征向量旋转。描述某个体的变化,就会变得十分方便。
此外,特征向量还有什么用呢?
我们思考一下,把如图矩阵乘个一百次,怎么算?
但是,如果我们用对角矩阵相乘,这样就会变得非常方便:
所以怎么把非对角矩阵转换为对角矩阵呢?
用特征向量。
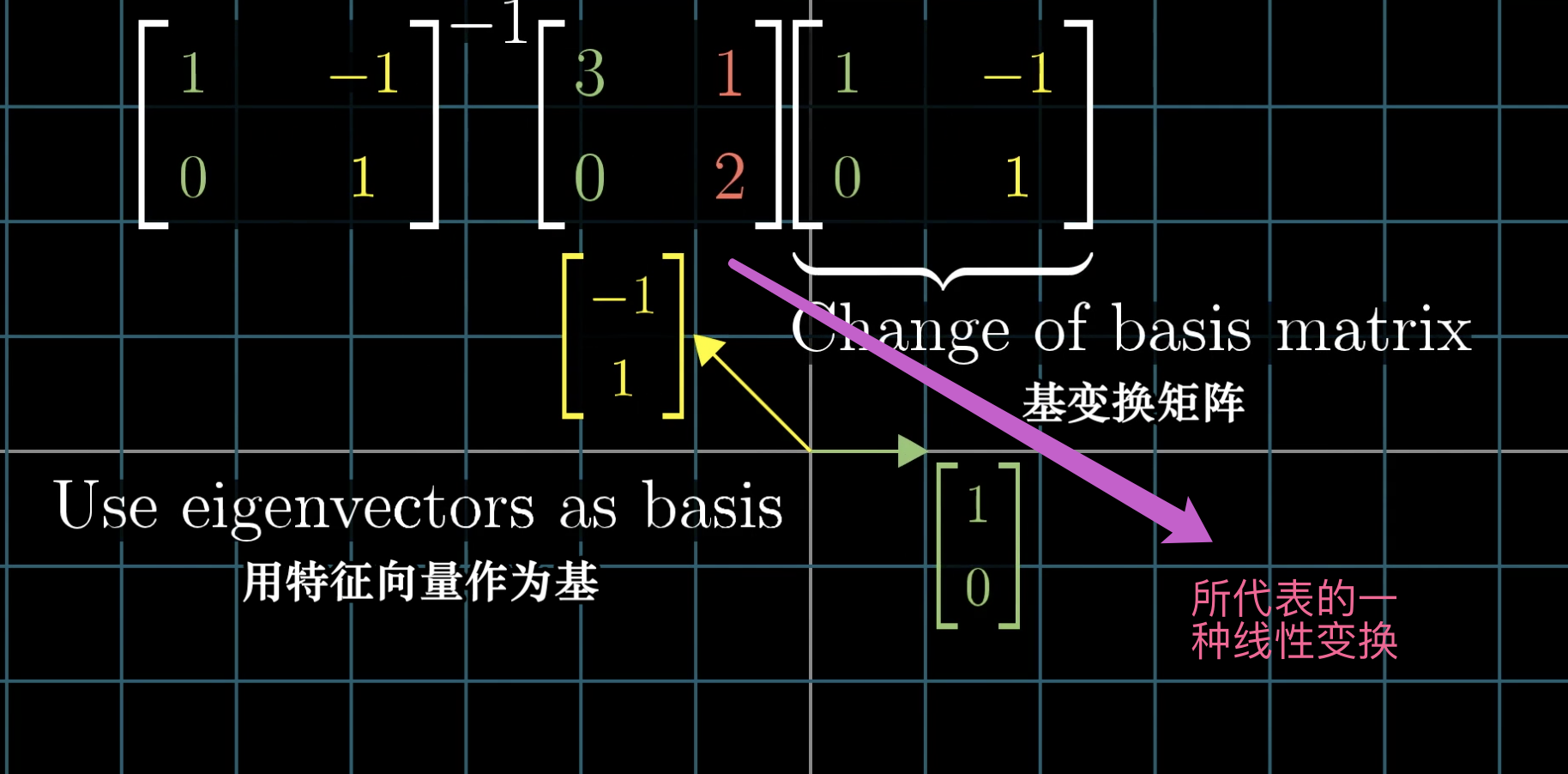
因为特征向量始终在自己张成的空间中变化,所以将其作为基最合适。
下面是用特征向量表示成基向量的方法。(这涉及到上一节(基向量)的知识)
结尾
The Essence 系列的每个视频开头都会有一段十分有趣的话






parallelepiped:平行六面体;俄语中发音为“帕拉丽丽匹珀斯”
- 本文作者: YA
- 本文链接: https://shiyuang-scu.github.io/2018/04/21/The-Essence-of-Linear-Algebra/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!


