零《SICP》笔记：构造过程抽象

2018-07-23

字数统计: 2.2k字 | 阅读时长≈ 9分

The acts of the mind, wherein it exerts its power over simple ideas, are chiefly these three: 1. Combining several simple ideas into one compound one, and thus all complex ideas are made. 2. The second is bringing two ideas, whether sim- ple or complex, together, and setting them by one another so as to take a view of them at once, without uniting them into one, by which it gets all its ideas of relations. 3. The third is separating them from all other ideas that accom- pany them in their real existence: this is called abstraction, and thus all its general ideas are made.
—John Locke, An Essay Concerning Human Understanding (1690)

第一章构造过程抽象

这章准备学习的是有关计算过程的知识。

什么是计算过程？计算过程是一种能操控称之为数据的抽象事物而进行本质上由数值运算构成的一系列进程的过程。程序员就像巫师念出一串咒语——他们编出一系列程序来作为计算过程的准则，来规范和指导计算过程的进行。

程序设计的基本元素

任何一种程序设计语言都必须要有三个机制作为基础：

基本表达形式
组合的方法
抽象的方法

三要素

基本表达式：

这样说过于翻译腔，其实很好理解，所为基本表达形式，就是基本表达式，包括诸如“+”，“-”，“*”，“/”一类内嵌于编程语言中的基本操作。

组合的方法：

将表达式用“（）”集合起来，形成符合表达式，比如
（+ 1 2）
输出就是

像这样的表达式称为组合式，在Lisp中，操作符总是出现在最左边，而后面出现的则是操作对象，一般都是数字。

抽象的方法

在Lisp中，给事物命名通过define操作来实现。比如：

1	(define size 2)

会告诉解释器，将2与“size”相关联，size称为表示值2的另一种方式。

define是我们所用语言中做简单的抽象方法，它允许解释器用一个名字来引用一系列很复杂的组合运算结果，来简化程序构造过程。

复合过程

我们已经可以通过Lisp看到某些元素，这些元素必然也会出现在其他编程语言中。这些元素包括：

Numbers and arithmetic operations are primitive data and procedures.
Nesting of combinations provides a means of combining opera- tions.
Definitions that associate names with values provide a limited means of abstraction.

define可用于另一种定义：过程定义

我们想想，如何实现“平方”这个概念？在Lisp中，应该这样实现：

1	(define (square x) (* x x))

这样我们就实现了一个复合过程，x作为局部变量，square x是 x平方操作的引用，我们将x平方定义为sqare x 后，就能将它作为基本元素应用在其他任何地方。

过程作为黑箱抽象

这一思想本质即追求简化，避免错误，减少工作量。举个例子，我们现在要求x的平方根，程序如下：

(define (sqrt x) 
	  (sqrt-iter 1.0 x))
	  
(define (sqrt-iter guess x) (if (good-enough? guess x)
      guess
      (sqrt-iter (improve guess x) x)))
      
(define (improve guess x) 
	  (average guess (/ x guess)))
	  
(define (average x y) 
	  (/ (+ x y) 2))
	  
(define (good-enough? guess x)
	  (< (abs (- (square guess) x)) 0.001))

sqrt是我们用手工定义的过程来实现的计算过程，这个程序可以看做一个树形结构：

Tree Structure

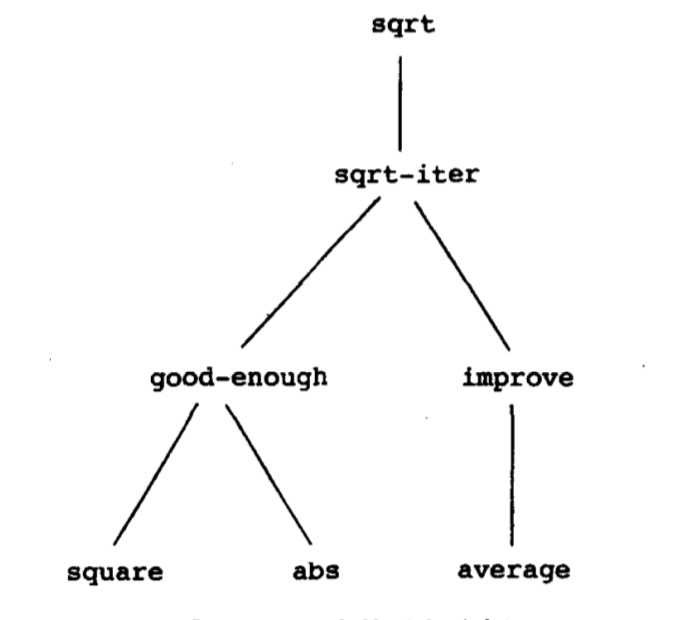
将一个大问题分解为一个个小问题，sqat作为一个黑箱，是一个过程的抽象。我们不需要在意sqrt-iter实现了什么操作，我们只需要把它作为一个黑箱，有输入输出即可。

我们还可以将定义内部化，形成嵌套的定义，如：

(define (sqrt x)
	(define (good-enough? guess x)
		(< (abs (- (square guess) x)) 0.001))
	(define (improve guess x) (average guess (/ x guess))) 
	(define (sqrt-iter guess x)
		(if (good-enough? guess x) guess
        (sqrt-iter (improve guess x) x)))
  	(sqrt-iter 1.0 x))

因为x作为局部变量，已经在开头定义过了，所以内部定义再定义x，是没有必要的，所以可以改进为：

(define (sqrt x)
	(define (good-enough? guess)
		(< (abs (- (square guess) x)) 0.001)) 
	(define (improve guess)(average guess (/ x guess))) 
	(define (sqrt-iter guess)
		(if (good-enough? guess) guess
        (sqrt-iter (improve guess))))
  	(sqrt-iter 1.0))

以上的定义称之为块结构

过程与它们所产生的对象

程序机制<——>程序行为

——>代换模型（正则序）

递归：time = O(X)

space = O(X)

迭代：time = O(X)

space = O(1)

迭代和递归的区别？

Diffenrance

（编程实际上是在编写一种通用规则）

递归过程——递归计算过过程

scheme特点：尾递归

什么是尾递归：

函数式编程非常重要的一个概念是递归。在函数式编程里面，递归是原生的合乎情理的，是从lambda计算继承而来的；而迭代（循环）是不良的，因为它的副作用，因为迭代（循环）意味着修改变量的值，违背了函数式编程的本意。修改变量的值是某些纯粹的函数式编程语言所坚决摈弃的，比如haskell。而scheme采取了更务实的做法支持修改变量的值，并且保留了迭代（循环）的语法。这是非常有趣和值得探讨的。我们知道，当一个函数的返回语句是另一个函数的直接调用，可称为尾调用tail call。尾调用的优点是节省程序运行时间和空间。因为函数每一层的嵌套调用，都意味着一个新的栈帧stack frame。栈帧保留了诸如实参值，局部变量，访问链，返回地址等信息，构造和销毁栈帧是程序运行时的开销。而尾调用，可以避免在内存中保留caller函数的栈帧，只需要直接把caller的返回地址复制到callee的返回地址。一般情况下的尾调用，优势不明显，但是如果是层次非常多的递归调用，则可以大大发挥作用。这种递归叫做尾递归。优化后的尾递归，即直接传递返回地址的尾递归，与过程式编程的迭代（循环）类同。以阶乘为例：

1
2
3

(define (factorial n)
    (if (= n 0) 1
        (* n (factorial (- n 1)))))

这是非尾递归的阶乘。可以看出，每次递归调用，都要保留caller函数的栈帧，因为callee的返回值还要继续*n的操作才能返回caller的值。

1
2
3

(define (factorial n acc)
  (if (= n 0) acc
        (factorial (- n 1) acc*n)))

这是尾递归的阶乘。可以看出，每次递归调用，都是同一个函数的不同参数调用，不需要保存多个栈帧，只要有一个栈帧即可。

高阶函数

过程作为参数：

语法——> 公共模式

公共模式：

(define (sum term a next b) 

    (if (> a b) 

        0

        (+   (term a) 

             (sum term (next a) next b))))

一.求立方和

(define (inc n) (+ n 1)) 

    (define (sum-cubes a b) 

    (sum cube a inc b))

二.求和

(define (identity x) x) 

    (define (sum-integers a b) 

    (sum identity a inc b))

三.求莱布尼茨公式

(define (pi-sum a b) 

    (define (pi-term x) 

        (/ 1.0 (* x (+ x 2)))) 

    (define (pi-next x) 

        (+ x 4))

    (sum pi-term a pi-next b))

三种计算由于遵照同一种计算模式，故都可由我们自定义的sum公共模式来实现，而sum包含了next、term操作，即体现了“将过程作为参数”。

lambda表达式

我们发现，不同需求所使用的term和next不同，我们要定义不同的term和next，这样很麻烦，也耗内存。

在这种next、term是一次性的要求下，我们引入lambda表达式，也许会更加好。

举个例子，我们计算莱布尼茨公式，引入lambda表达式，可以这样做：

将next变成：

(lambda (x) (+ x 4))

将term变成：

1	(lambda (x) (/ 1.0 (* x (+ x 2))))

则计算莱布尼茨公式则为：

(define (pi-sum a b)

    (sum (lambda (x) (/ 1.0 (* x (+ x 2)))) 

         a

         (lambda (x) (+ x 4)) 

         b))

寻找一种公共的模式，这实际上是把过程进行了封装。如果我们运行刚开始提出的程序来求和，一旦需求改变，整个程序都得重写。但如果我们使用后面提出的程序，因为我们将sum这个过程进行了封装，所以无需改变其他与需求无关的程序，只要改sum就好了。

过程作为返回值

简单来说就是定义一个含有函数作为参数的另一个函数，比如：

1
2
3

(define (ave-damp f)

    (lambda(x) (average x (f x) ) ) )

就是把add f 定义为一个过程

In general, programming languages impose restrictions on the ways in which computational elements can be manipulated. Elements with the fewest restrictions are said to have first-class status. Some of the “rights and privileges” of first-class elements are:

They may be named by variables.
They may be passed as arguments to procedures.
They may be returned as the results of procedures.
They may be included in data structures.

Lisp, unlike other common programming languages, awards procedures full first-class status. This poses challenges for efficient implementation, but the resulting gain in expressive power is enormous.

本文作者： Yuang
本文链接： http://www.yuuuuang.com/2018/07/23/零-《SICP》读书笔记：构造过程抽象/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！

第一章 构造过程抽象