第二章 构造数据抽象
The acts of the mind, wherein it exerts its power over simple ideas, are chiefly these three: 1. Combining several simple ideas into one compound one, and thus all complex ideas are made. 2. The second is bringing two ideas, whether sim- ple or complex, together, and setting them by one another so as to take a view of them at once, without uniting them into one, by which it gets all its ideas of relations. 3. The third is separating them from all other ideas that accom- pany them in their real existence: this is called abstraction, and thus all its general ideas are made.
—John Locke, An Essay Concerning Human Understanding(1690)
数据抽象是一种方法学，它将程序要使用的复合数据与构成复合数据的基本数据和细节过程区分开来。
数据抽象导引
将数据封装，由单个数据转化成复合数据，其最终目的和之前将过程抽象化一样，是为了层次化的程序，将过程封装，以达到优化的目的。
实例：有理数运算
现在我们来设计一个有理数运算的程序，包括加减乘除，这时我们就会运用一种策略，称之为不要怂就是干，好吧我开玩笑的，叫愿望思维，很简单，即使你没有实现任何功能，也不要怂，管它有没有实现，先写个顶端代码再说。1
2
3
4(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
1 | (define (sub-rat x y) |
1 | (define (mul-rat x y) |
1 | (define (div-rat x y) |
我们其实完全没有实现make-rat、numer、denom这些过程，但我们虽然是因为没有完成工作而瞎写的，但无意之间却将每一种过程都抽象化，这实际上有利于程序的实现和维护，所以不要怂就是干愿望思维是很好的抽象方法。
下面来实现上面的过程：1
2
3
4
5(define (make-rat n d) (cons n d))
(define (numer x) (car x))
(define (denom x) (cdr x))
以上出现了Lisp新的数据结构，序对（pairs）
Lisp：表结构——序对1
2
3(cons x y)
(car p)
(cdr p)
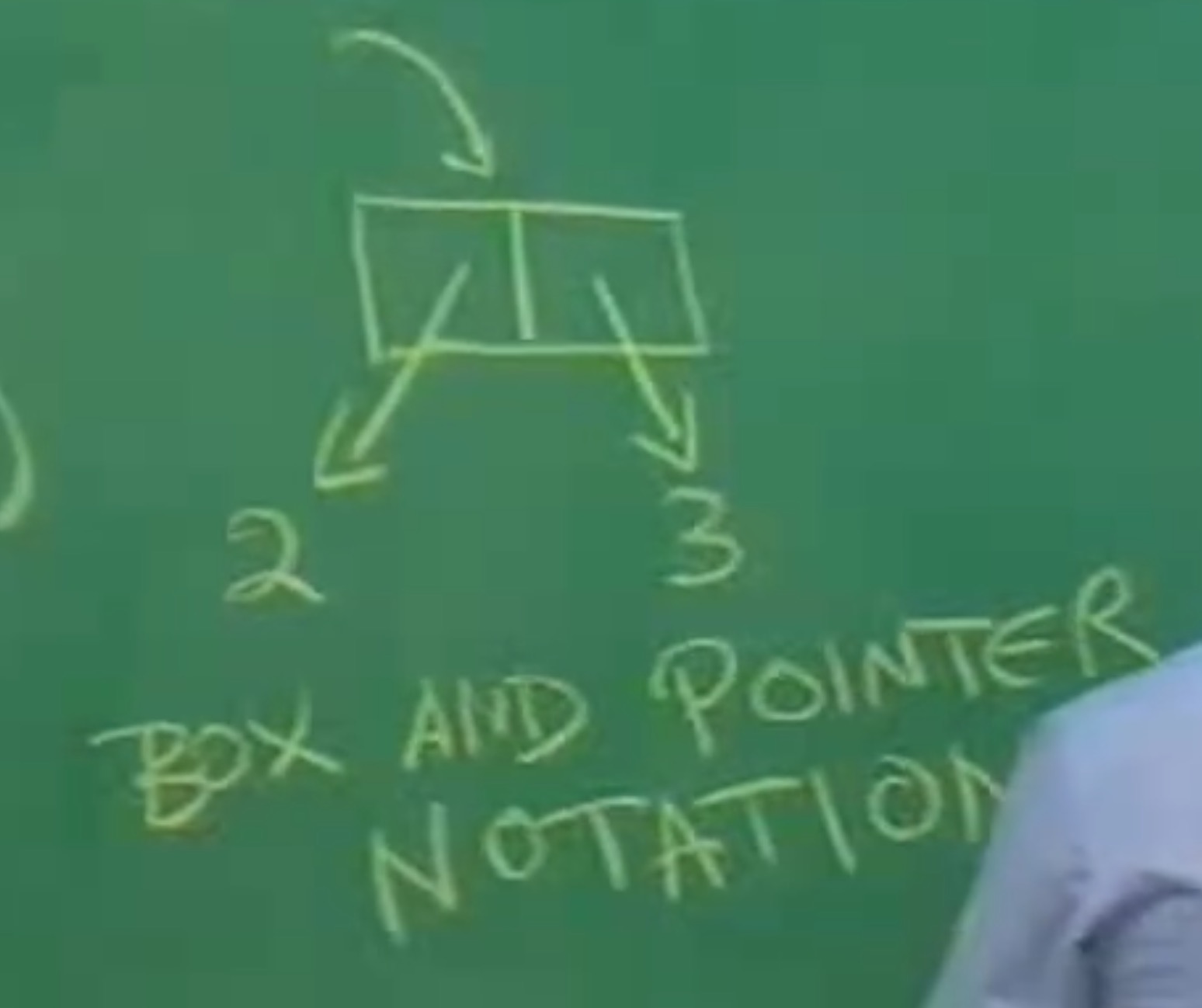
构造函数和选择函数作为抽象屏障(Abstract Barriers)，将数据的使用和表示分离开来。这样的模式被称数据抽象
数据抽象的目的也很简单，就是降低系统复杂度，便于维护和改进。
看有理数运算的例子，我们实际上把这个程序层次化为了四个结构，由构建序对依次向上堆积，层层封装，最后只要调用单纯的一个过程就能实现运算。
实例：点与线段
再举一个和有理数很像的例子，我们在平面上有一个点P(x,y)，我们可以用向量来表示这个点，(x,y)的结构让我们很自然地想到了序对：1
2
3
4
5(define (make-vector x y) (cons x y))
(define (xcor p) (car p))
(define (ycor p) (cdr p))
现在我们有两个点P、Q，我们要如何表示两个点构成的线段呢？很简单，两个点构成的一个抽象组合就能在一定程度上表达线段的位置，那么我们只要将两个向量放到一起就可以了：1
2
3
4
5(define (make-seg p q) (cons p q))
(define (seg-start s) (car s))
(define (seg-end s) (cdr s))
这样定义后，我们就可以很容易地进行和这条线段有关的操作了，比如求线段中点：1
2
3
4
5
6
7
8
9
10
11(Define (midpoint s)
let ((a (seg-start s))
(b (seg-end s)))
(make-vector
(average (xcor a) (xcor b))
(average (ycor a) (ycor b))))
两个例子都在强调，设计系统时要注意将系统分层，每一层之间的抽象屏障都有特定的构造函数和选择函数来组成，比如有理数运算中的make-rat与xcor和两点中点运算中的make-vector与numer。
所以我们可以自上而下地理解，层次系统要求我们对数据进行复合和封装，否则就会出现混乱乃至系统失控。
闭包（closure）
有权访问另一个函数作用域内变量的函数都是闭包。
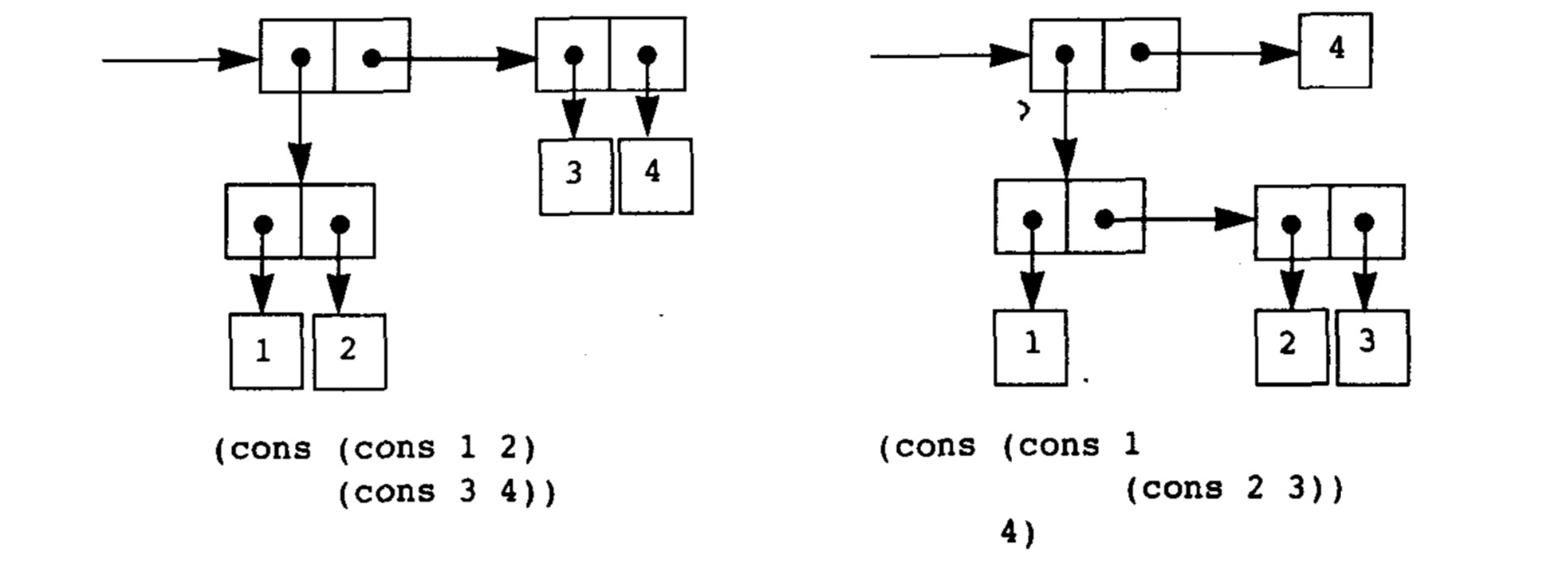
在以上例子中，一个序对内部的两个元素依然是序对，这种可以用同样方法把组合物继续进行组合的模式，就叫做闭包性质。
就拿我们定义一条线段的例子吧，我们将两个向量组合为一个向量，运用了Lisp中的cons，这种序对中的序对，即是把通过cons操作构成的组合物（序对）继续进行组合（将两个序对包装到一个序对里去）的模式。
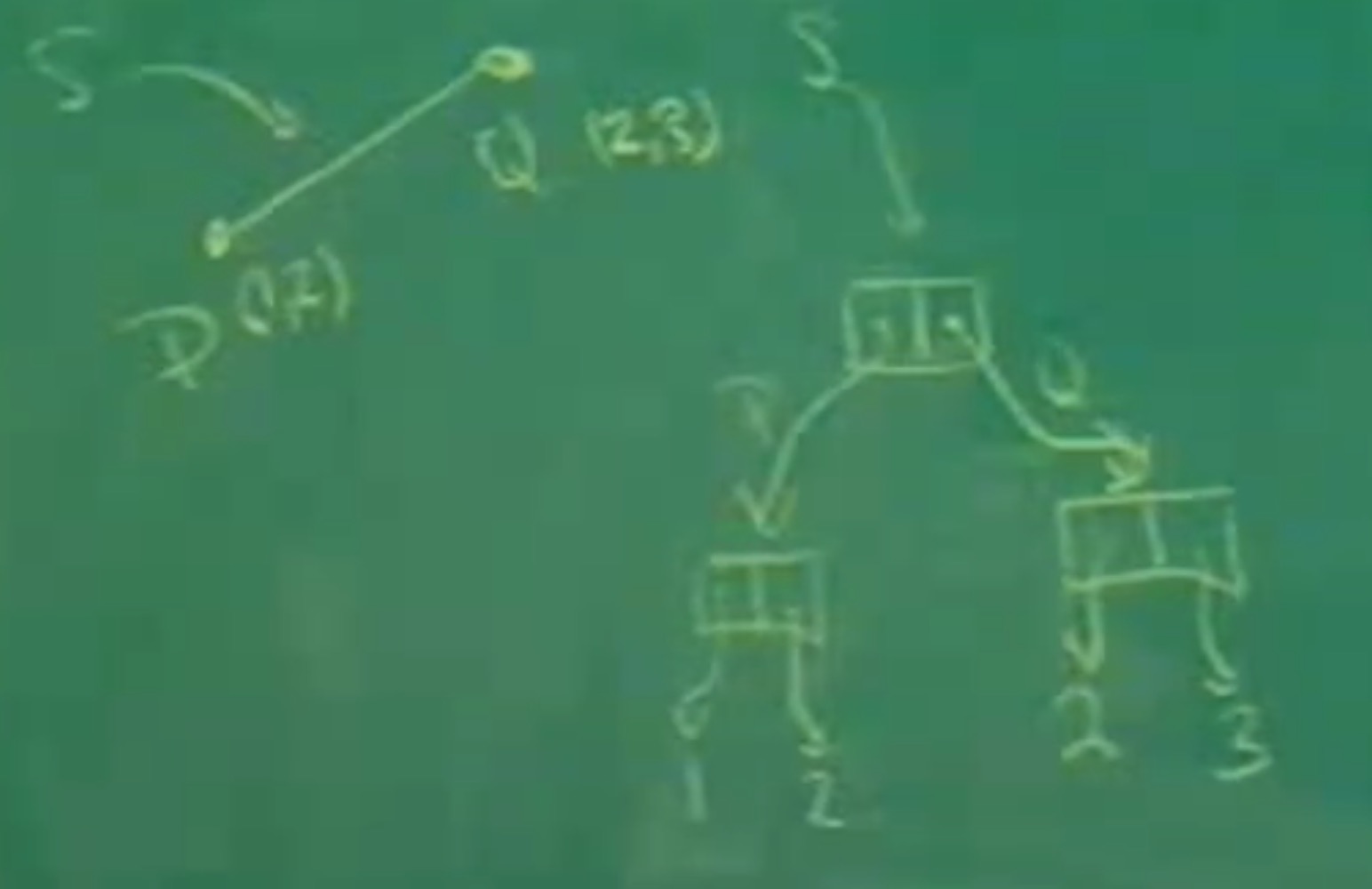
从上一章开始，你也许慢慢发现了，数据与过程之间的界限越来越模糊，过程可以作为形参存在，而复合数据或者说数据的抽象化也必须由过程来实现，其实，不必感到困惑，数据与过程之间的界限模糊是抽象化的必然结果。
层次性数据与闭包性质
经典作品是一些产生某种特殊影响的书，它们要么自己以遗忘的方式给我们的想像力打下印记，要么乔装成个人或集体的无意识隐藏在深层记忆中。
—卡尔维诺《为什么读经典》
数据组合规范：链表
我们将数据组合起来，组合方式有很多，举个例子，我们有数据1、2、3、4，在没有规定的情况下，可以有很多组合：
因此就需要有一个统一的规定来处理这样的数据组合，在Lisp中称之为链表。
本质上链表就是处理一系列序列数据的一个约定，在scheme中的实现需要借助于序对。我们将1、2、3、4使用list的表现形式实现如下：
1 | (define （1-TO-4） |
结尾的nil是拉丁文nihil的缩写，意为什么都没有，也许我们用null会更熟悉。
1-TO-4的过程，直观地来看，是这样的：
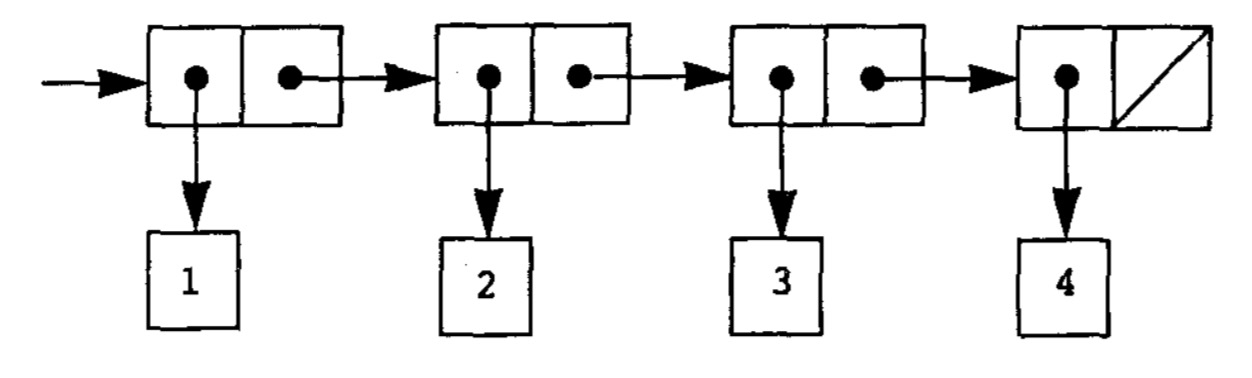
具体在链表中的操作，我们是通过car、cdr来实现的：
在Scheme中，为了方便，链表的表示已经被封装成名之list的基本数据操作，这同样显示了抽象屏障：我们不需要知道怎样用cons实现了List，我们不要cons那倒霉孩子，我们只要乖巧听话的list。
所以，我们刚刚定义的“1-TO-4”的过程，就可以用(list 1 2 3 4)来表示
表操作
我们可以用链表的cdr与car操作来对每个元素进行同一操作，举个例子，我们现在要把一串链表的数据进行缩放，我们这样做：1
2
3
4
5(define (scale-list s l)
(if (null? l)
nil
(cons(* (car l) s)
(scale-list s (cdr l)))))
其中l为链表，s为缩放参数
再次感慨，递归真是一种强大的工具
还记得之前我们讲的将过程抽象吗？对这种将链表数据统一操作的过程，我们可以将其抽象化，这种抽象化的操作在Scheme中称为map，那么如果我们将想对list元素进行操作的过程称之为p，那么p通过map来实现，这个过程表达为如下形式：1
2
3
4
5(define (map p l)
(if (null? l)
nil
(cons (p (car l))
(map p (cdr 1)))))
By the way，还有一种与map类似的方法，称之为for-each：1
2
3
4
5(define (for-each proc list)
(cond (null? list) "done")
(else (proc (car list))
(for-each proc
(cdr list)))))
事实上，for-each的计算方法不是递归，而是迭代。
我们能使用闭包的性质快速增加复杂度
组合的方法就是构造过程
通用方法抽象为高阶过程
过程与数据在抽象过程中没有任何区别
计算机领域有一种方法学（methodology）或者说是“神话学”（mythology），叫做软件工程。软件工程师坚信，完成一项软件工程，一定要清楚了解我们要做什么，将各个任务分解成一个个更小的任务，构造成一个类似树的结构，树中的每个节点都被严格定义，我们从最小的节点开始，逐一解决，最后构建成整栋大厦。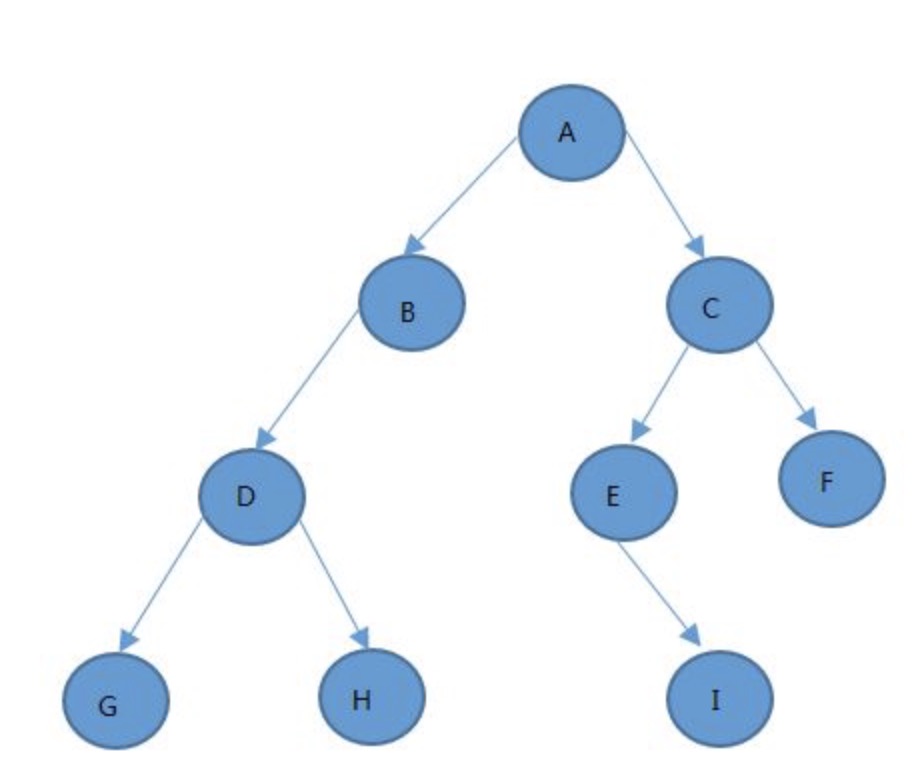
但好的工程系统也许不是这样的。好的工程系统应该有一个层次序列，每一块都是一个完全的、闭合的整体，从底层开始，以前一块为基础向上搭建，逐渐抽象，抽象过程一块与一块紧密而非耦合地联系在一起。
图为教授朋友构造的一种基于Lisp语言而制作的处理图像的另一种语言（见IBM的SICP公开课Lec3a-Escher的例子
两者有什么区别呢？前者，即树形结构每一个节点的分解都旨在分解，而后者的每一个层级都是一个完全意义上的独立抽象层。换句话说，前者的每一个节点意在完成特定的任务，而后者则将整个过程抽象化，它讨论的不是具体的事，而是整个事件。因此，后者会比前者更具有鲁棒性（robust），当我们改变一个细微的要求时，后者会更加轻易地适用于改变，而前者却会因为这个细小的改变而被摧毁重建。
换一个角度，我们甚至可以这样思考：鉴于一种语言的基本要素为基本数据、数据组合、过程抽象，这种层次序列的构建实际上是在一种语言的基础上设计了另一种语言，或者说是在一种语言中嵌入（embed）了另一种语言。
Lisp的设计表达了一个不同于软件工程学的观点：真正的设计过程，不是在设计程序，而是在设计语言。
符号数据
上一节我们知道，对于一个工程，不要依次解决子问题，而要将问题抽象化，抽象化的结果是，以一种方法解决了所有具有相同模式的问题。
我们之前的抽象，都是在抽象对数值处理的过程，而非对数值抽象化为符号。例如我要求和，我们define一个add过程，即抽象化了求和这个过程，但其参数一定是数值，要不然就无意义。但数值是特定的，无法抽象化，所以符号数据就很自然地被引入了。
引号
如果你问我：“说出你的名字！”，我会毫不犹豫地说，“XXX”，但如果你一脸不耐烦，反复地问我，“说出你的名字！”，我会想看智障一样看着你，或许会突然开窍，向你大喊：“你的名字！！！！”。对，这就是引号给我们带来的歧义。
“说出你的名字”这句话实际上是存在很大歧义的，你可以理解为正常的“说出你的名字”，但也可以理解为“说出 ‘你的名字’ ”。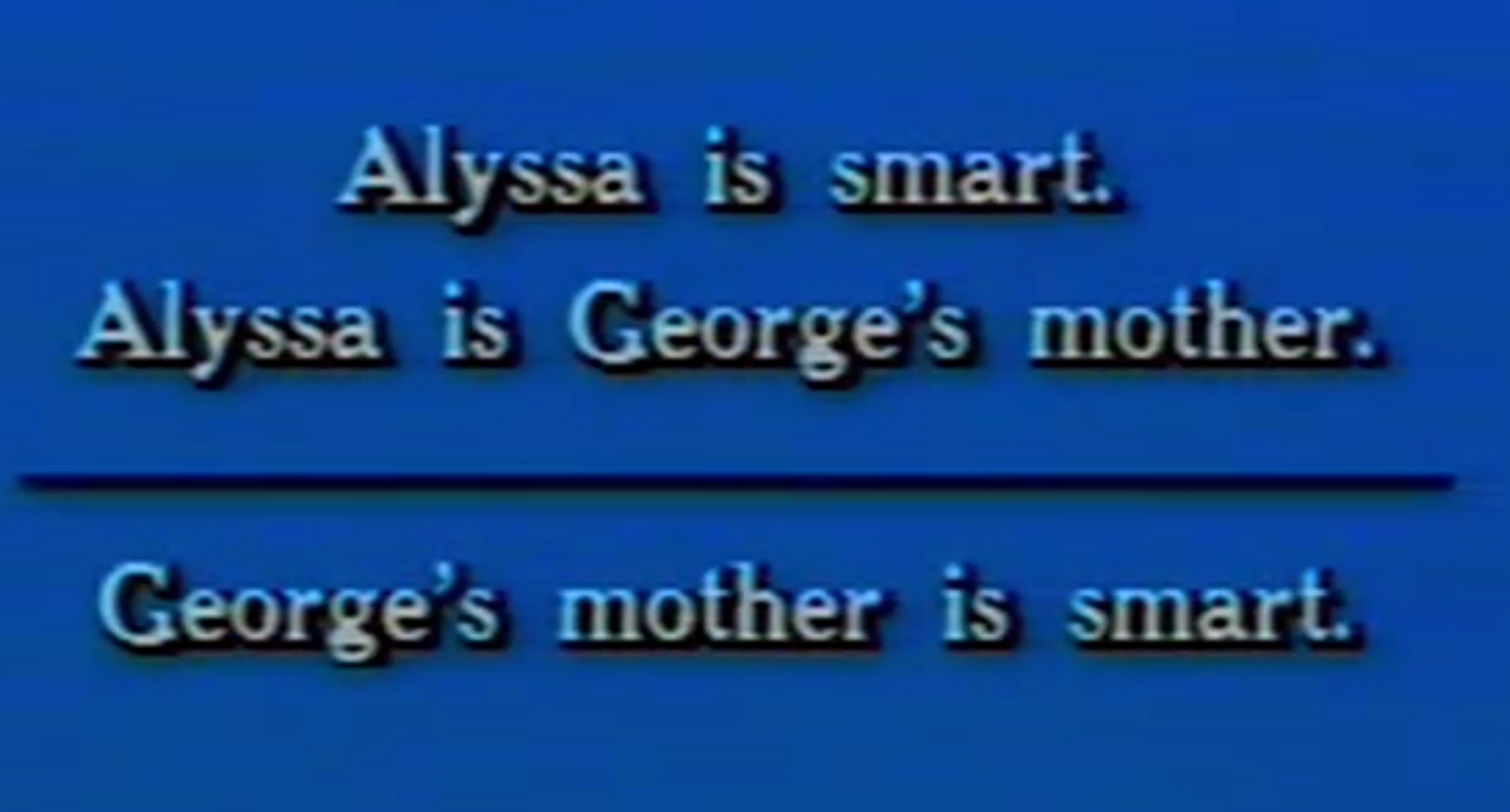
如图，“is”作为谓词，在这几句话中实质是“=”，或者说是进行了赋值操作，所以我们可以联立两个等式，最后得出George的妈妈很聪明的结论。但如果将谓词后面的内容改成引号，那么所谓的“is”就绝不是赋值这么简单了。
如果我们想构造出表示符号数据的运算操作，比如 aa+b ，我们可以将这个表达在LIsp中表示成1
(a * a + b)
怎么样都行，但我们一般会用Lisp中的运算惯例：1
(+ (* a a) b)
现在我们可以区分符号与数值，比如以下代码：
引号也可用于复合过程：
1 | (car '(a b c)) |
其结果是：1
a
而1
(cdr '(a b c))
其结果是：1
(b c)
从以上代码可以看到，引号确实是构建了一个包含符号的链表。
放一张图自己体会：
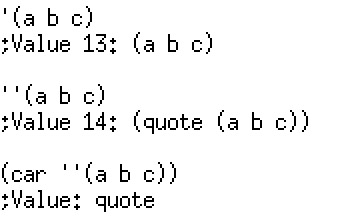
符号操作实例：符号求导
再一次膜Lisp
求导和求积分互为逆过程，但为什么求导容易而求积分难？
因为求导是一种归约过程，可用递归解决，而求积分则会出现很多种可能情况。
当然，以上是题外话，下面进入正题：
为了更好地阐述符号操作，我们准备实现一个代数表达式的符号求导过程。
使用愿望思维，我们可以构建出以下过程：
这也显现了符号数据的优势，即，抽象，抽象，再抽象。
（……）这样的形式，就是链表，我们可以通过链表的形式来表示一串代数表达式。
因为符号数据不存在诸如“+、-“的运算机制，所以需要我们自己构造，这在介绍引号那一节已经说明过了。
所以，之前实现求导过程中没有实现的函数，可以这样表示：
就这样，我们完美地实现了代数表达式的符号求导过程。
我们不厌其烦的强调了这一点：抽象。
以上的过程构造同样重复了抽象屏障：
==求导法则==
↑
==接口过程==
↑
==表结构==
注：为什么叫“CAR”“CDR”？
The popular explanation that CAR and CDR stand for “Contents of the Address Register” and “Contents of the Decrement Register” does not quite match the IBM 704 architecture; the IBM 704 does not have a programmer-accessible address register and the three address modification registers are called “index registers” by IBM.
The 704 and its successors has a 36-bit word length and a 15-bit address space. These computers had two instruction formats, one of which, the Type A, had a short, 3-bit, operation code prefix and two 15-bit fields separated by a 3-bit tag. The first 15-bit field was the operand address and the second held a decrement or count. The tag specified one of three index registers. Indexing was a subtractive process on the 704, hence the value to be loaded into an index register was called a “decrement”. The 704 hardware had special instructions for accessing the address and decrement fields in a word. As a result it was efficient to use those two fields to store within a single word the two pointers needed for a list.
Thus, “CAR” is “Contents of the Address part of the Register”. The term “register” in this context refers to “memory location”.
- car ( “Contents of the Address part of Register number”),
- cdr (“Contents of the Decrement part of Register number”),
抽象数据的多重表示
通用型过程
我们之前一直在试图实现的，是实现数据对象与对数据对象操作的分离，关键性思想就是构建抽象屏障，比如之前说过的有理数运算，通过有理数的选择函数与构造函数，将有理数的构成与操作分离开来。
从另一个角度看，一个数据常常会有不同的表示方法，而将同一操作应用于不同的构成方式，则成为这一节的重点。即构建通用型过程。
我们将以复数的运算为例。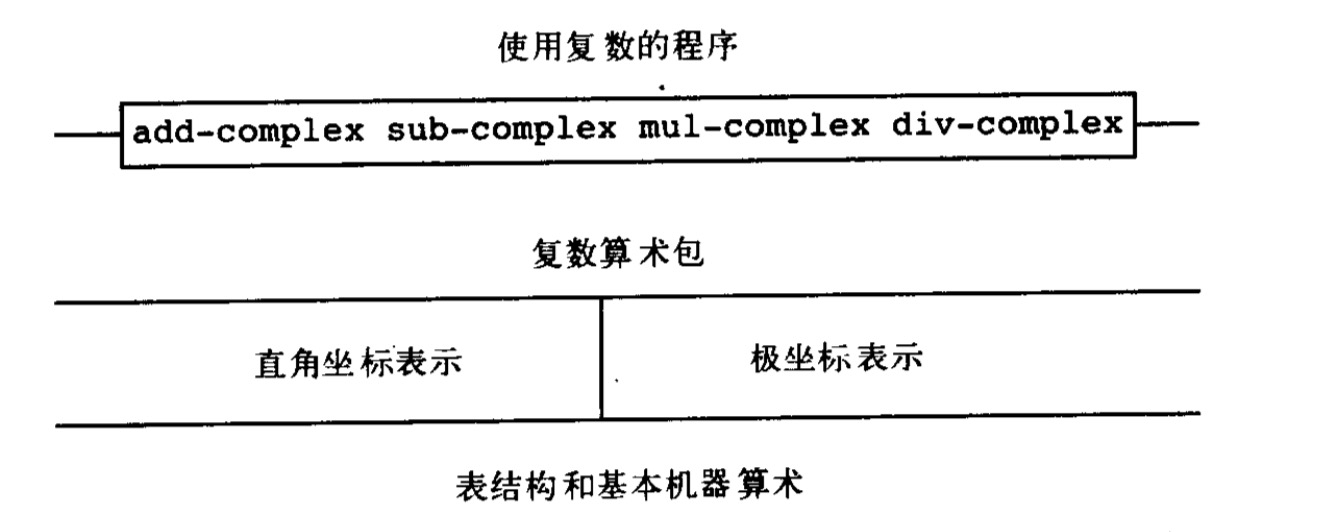
这是构建复数运算的抽象屏障
复数有两种表示形式，直角坐标系与极坐标系，构造函数则为：make-from-real-imag和make-from-mag-ang，分别返回一个采用实部与虚部描述的复数、采用模和幅角描述的复数。选择函数为：real-part、imag-part、magnitude和angle。
则复数算术就可以实现了：
为了完成这样的运算，我们首先得把两种负数的表示形式转化为其中一种，这样，在接受input数据的时候，就能将其转化为其中一种，统一进行运算。
问题在于，系统得识别input属于哪一种表示方式，所以，就自然而然地出现了类型标志。类型标志用以区分不同的表示方式，在复数算术运算中，标识符为rectangular和polar。
每个通用型选择函数都得实现这样的过程：检查参数的类型标志——>调用合适的过程来处理数据
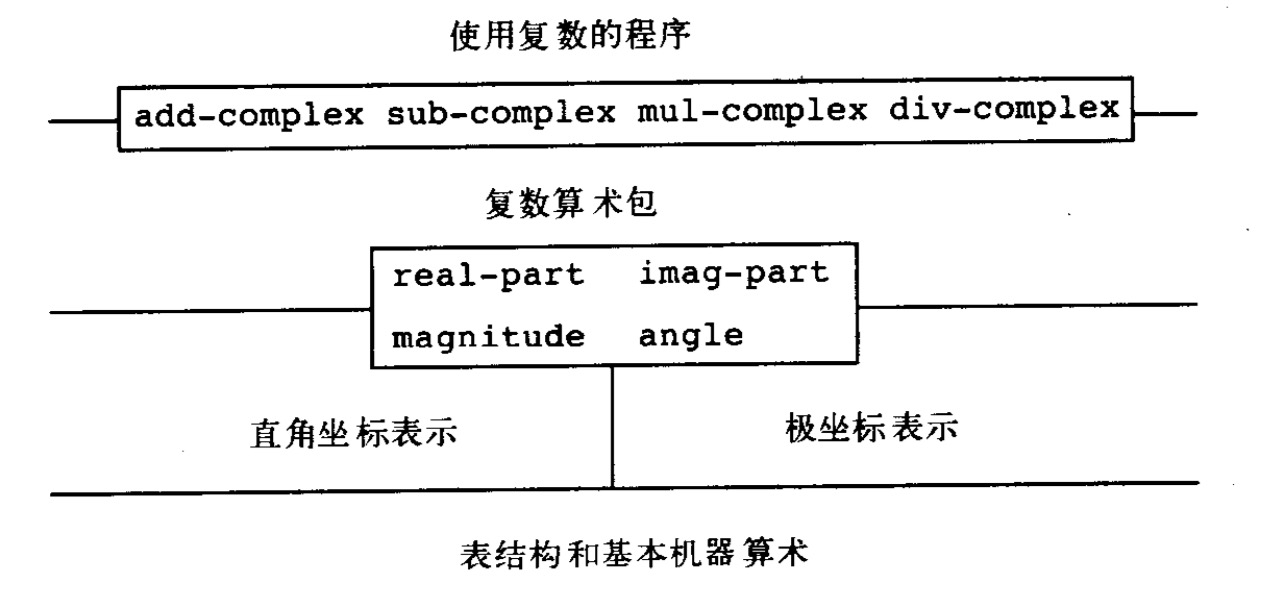
这样，直角坐标系与极坐标系两部分就可由第三部分：real-part等一系列选择函数实现。也就是相当于，整个选择过程被完整地封装成了三个部分，交给了三个程序员去完成。
第三部分可以理解为通用型界面过程。
数据导向
刚刚的策略被称为基于类型的分派，但其存在一定的漏洞和缺点：通用型界面过程必须依赖所有可能性来进行决策，比如我增加了一种新的形势表示复数，我就需要在每一个通用型过程中增加一个选择语句来将这一表示方式转换成统一方式，假如我有成百上千种方式，复杂度就会蹭蹭上涨。
一句话，基于类型的分派不具有可加性。
因此引入了数据导向。
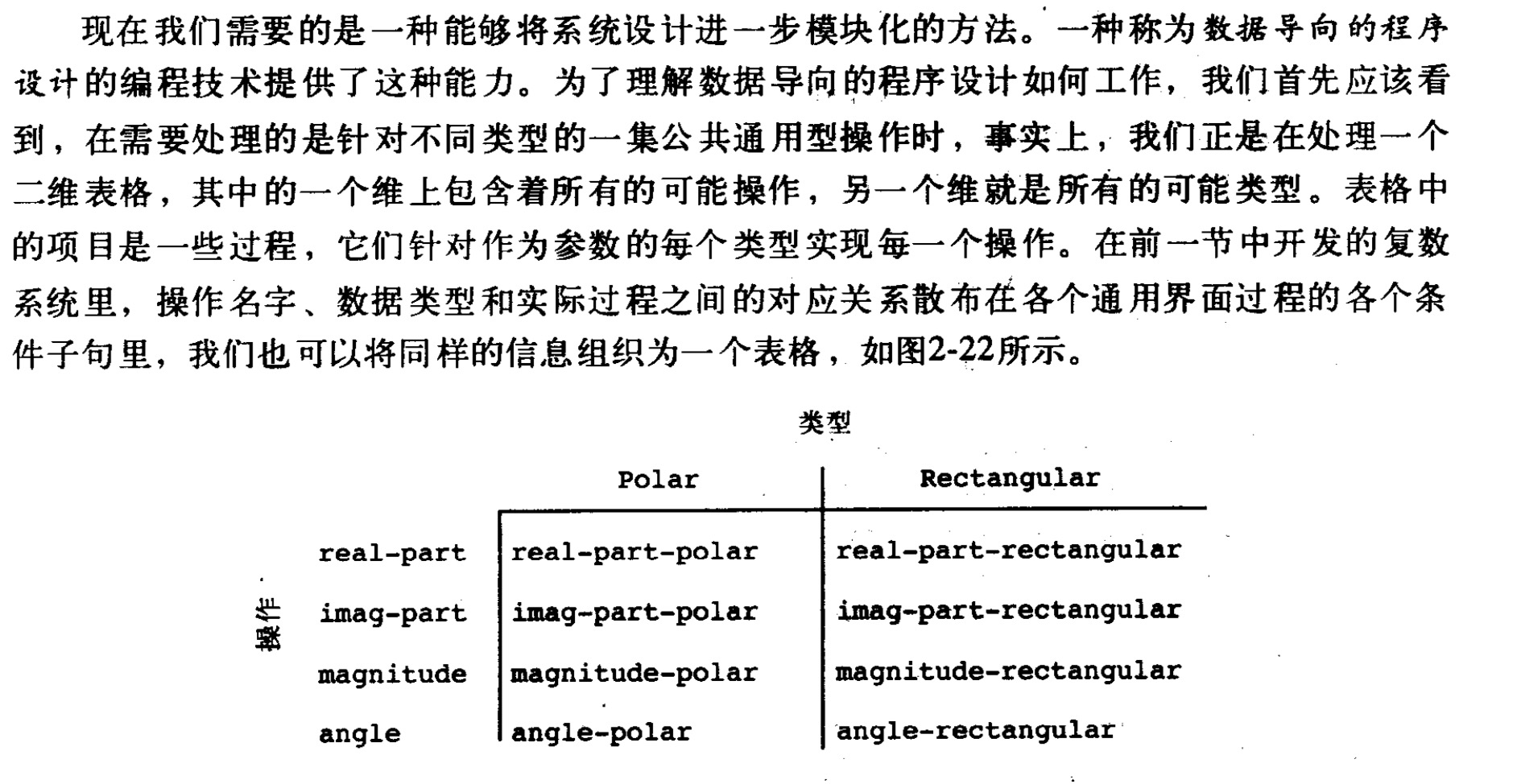
所谓数据导向，就是借助于这张二维表，构建一个类似于索引的过程。如果加入新的表示形式，我们只要增加一列索引即可。具体操作如下：
举个例子，我们可以定义两个程序包，分别是负数的两种表示形式，在直角坐标系包中，给real-part的操作过程增加两个名称的索引：’polar 和 ‘real-part，意思就是把在直角坐标系中把极坐标系转换成直角坐标系的real-part过程赋予两个名称索引。
我们再定义一个操作访问表格，返回有关操作：
带有通用型操作的系统
- 本文作者： Yuang
- 本文链接： http://www.yuuuuang.com/2018/08/01/壹-《SICP》笔记：构造数据抽象/
- 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！