Softmax Regression

阅读数：21870次 2018-09-08

字数统计: 1.2k字 | 阅读时长≈ 4分

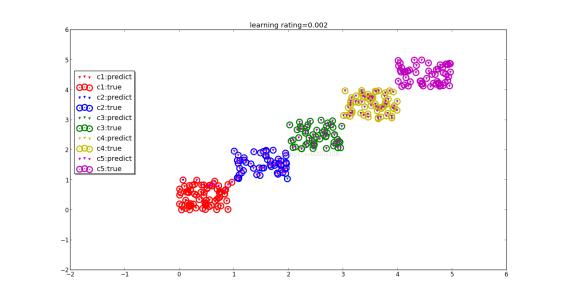
Softmax-0

Abstract

Softmax Regression是Logistic Regression的推广

LR能做的是区分两类，而SR则能区分n类，虽然两者的本质都是线性的

Logistic Regression的回顾

对于数据集{(x^1,y^1) , … , (x^m,y^m)},y只有两个类别，我们记为{0,1}，LR的假设函数(hypothesis function) 如下：

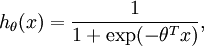
$Softmax-1$

我们的目的是训练参数theta，使得可以拟合原数据集，则代价函数为：

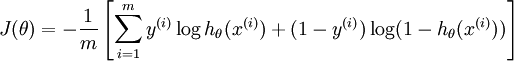
$Softmax-2$

假设函数

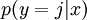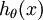对于给定的测试输入 $\textstyle x$ ，我们想用假设函数针对每一个类别j 估算出概率值 $\textstyle p(y=j | x)$ 。也就是说，我们想估计 $\textstyle x$ 的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个 $\textstyle k$ 维的向量（向量元素的和为1）来表示这 $\textstyle k$ 个估计的概率值。具体地说，我们的假设函数 $\textstyle h_{\theta}(x)$ 形式如下：

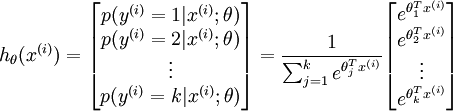
$Softmax-3$

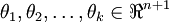其中 $\theta_1, \theta_2, \ldots, \theta_k \in \Re^{n+1}$ 是模型的参数。请注意 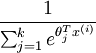$\frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} }$ 这一项对概率分布实际上进行归一化，使得所有概率之和为 1，这也是Softmax分类器的精髓。

代价函数

回望Logistic Regression，我们的代价函数中，有(1-y^i)和(y^i)原因就在于，y只能是0或者1，所以在计算代价的时候，能够用这种形式来去除不属于y=0或者1的结果。但是在Softmax中，y不只是等于0、1了，所以我们这样定义：

在下面的公式中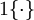， $\textstyle 1\{\cdot\}$ 是示性函数，其取值规则为：

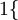$\textstyle 1\{$ 值为真的表达式}=1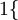， $\textstyle 1\{$ 值为假的表达式 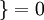$\textstyle \}=0$ 。举例来说，表达式 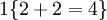$\textstyle 1\{2+2=4\}$ 的值为1 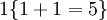， $\textstyle 1\{1+1=5\}$ 的值为 0。我们的代价函数为：

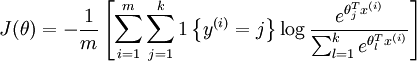
$Softmax-4$

值得注意的是，上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为：

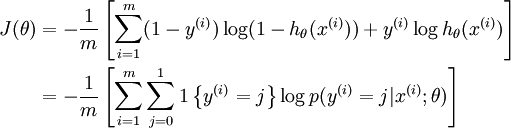
$Softmax-5$

可以看到，Softmax代价函数与logistic 代价函数在形式上非常类似，只是在Softmax损失函数中对类标记的 $\textstyle k$ 个可能值进行了累加。注意在Softmax回归中将 $\textstyle x$ 分类为类别 $\textstyle j$ 的概率为：

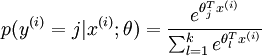
$Softmax-6$

对于 $\textstyle J(\theta)$ 的最小化问题，目前还没有闭式解法。因此，我们使用迭代的优化算法（例如梯度下降法，或 L-BFGS），步骤和在LR中的一样。

参数冗余

Softmax有一个很神奇的特性，它存在参数冗余。什么意思呢？举个例子：

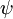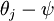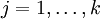假设我们从参数向量 $\textstyle \theta_j$ 中减去了向量 $\textstyle \psi$ ，这时，每一个 $\textstyle \theta_j$ 都变成了 $\textstyle \theta_j - \psi$ ( $\textstyle j=1, \ldots, k$ )。此时假设函数变成了以下的式子：

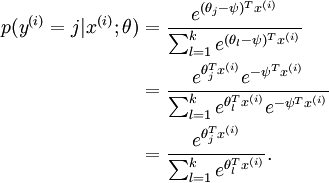
$Softmax-7$

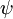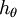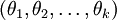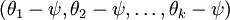换句话说，从 $\textstyle \theta_j$ 中减去 $\textstyle \psi$ 完全不影响假设函数的预测结果！这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说， Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数，可以求出多组参数值，这些参数得到的是完全相同的假设函数 $\textstyle h_\theta$ 。具体来说，如果参数 $\textstyle (\theta_1, \theta_2,\ldots, \theta_k)$ 是代价函数 $\textstyle J(\theta)$ 的极小值点，那么 $\textstyle (\theta_1 - \psi, \theta_2 - \psi,\ldots, \theta_k - \psi)$ 同样也是它的极小值点，其中 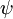$\textstyle \psi$ 可以为任意向量。因此使 $\textstyle J(\theta)$ 最小化的解不是唯一的。

那我们可以直接把 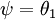$\textstyle \psi = \theta_1$ 嘛，这样一来，原本是 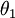$\textstyle \theta_1$ 的地方就变成了0，式子简化了不少。

接下来我们就利用参数冗余这个特点，来推导SR其实就是LR的普遍形式，LR是SR的分类数n=2时的特殊情况这个结论。

当 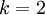$\textstyle k = 2$ 时，softmax 回归的假设函数为：

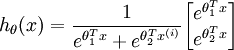
$Softmax-8$

利用softmax回归参数冗余的特点，我们令 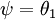$\textstyle \psi = \theta_1$ ，并且从两个参数向量中都减去向量 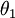$\textstyle \theta_1$ ，得到:

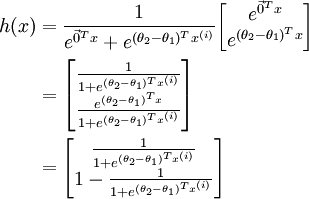
$Softmax-9$

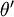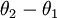因此，用 $\textstyle \theta'$ 来表示 $\textstyle \theta_2-\theta_1$ ，我们就会发现 softmax 回归器预测其中一个类别的概率为 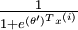$\textstyle \frac{1}{ 1 + e^{ (\theta')^T x^{(i)} } }$ ，另一个类别概率的为 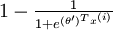$\textstyle 1 - \frac{1}{ 1 + e^{ (\theta')^T x^{(i)} } }$ ，这与 logistic回归是一致的。

SR与LR的使用场合

SR与LR的使用场合区别在于，分类的对象是否互斥。举个例子：以前世界上只有男性、女性和阉人，那么我们就可以用SR来做分类，因为三者是互斥的，不可能有人既是男人又是女人，或者既是男人又是阉人。

但是，若是依照奥巴马政府在“跨厕法”中提出的心理性别标准，即你生下来是男的，即使现在心理上认为自己是女性，就可以进女厕，反之亦然。那么一个人既可以是男性的女性，也可以是女性的男性，可能这个人前一段时间觉得自己是女性，后来又觉得自己是男性了。现在的类别包括：男性、女性、女性的男性、男性的女性，这四者不再互斥，那么我们就只能用4个LR来作区分。

Reference：

Softmax回归
 理解softmax分类器

本文作者： YA
本文链接： http://www.yuuuuang.com/2018/09/08/Softmax-Regression/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！