2018.11.3创建
2018.12.9更新
2018.12.10更新
2018.12.11完稿
本篇介绍了Policy Gradient的结构、算法,以及优化
Q :Policy Gradient和Q-Learning的区别在于,前者直接选择动作,后者根据奖惩值选择动作。Q-Learning的方法,通俗点来说,就是哪个动作更有好处,就选择哪个。但是,PG在选择动作上的策略在本质上不也是因为这个动作更有好处吗?所以不还是需要一个类似奖惩值来供参考吗?
A:第一句话的后半句说得没错,但前半句就错了。PG和QL的区别在于,QL是基于贪婪算法的,具体地说,就是将每一个目标分成一个个小目标,只要把小目标做得好,大目标就做好了,所以QL做的是优化每一个小目标,而不管大目标怎么样;PG则倒过来,它不管小目标怎么样,他只关心大目标——只要大目标完成好了,之后就多多用完成大目标的这种方法,如果大目标完成不好,那这种方法就给它打入冷宫。
为什么是PG,而不是QL?
QL的输入是动作和状态,输出的是奖励值(评判在这种状态下做出这种动作是好是坏的分数),所以我们要把所有在该状态下可能的动作做一遍得到每个动作的奖励值,然后选择奖励值最大的(在该状态下最有利的动作)。因为这种性质,所以QL算法得到的策略不具有整体观——因为它选择的是每一个对当前状态最有利的行为。所以本质上QL也就是贪婪算法。
PG的输入是状态,输出是动作,是端对端的算法,更加直观而且更具有整体性。PG就是先不管三七二十一,随机来个100套动作试一试,其中有的一套做得好,有的做得不好,这一套动作做得好,就加分,增加下次做这套动作的可能性;那一套动作做得不好,就扣分,下次就尽可能不做这套动作了。这样下来,训练量多了,就大概知道什么状态下该做什么了。
正如Karpathy在其博文中写的:
It turns out that Q-Learning is not a great algorithm (you could say that DQN is so 2013 (okay I’m 50% joking)). In fact most people prefer to use Policy Gradients, including the authors of the original DQN paper who have shown Policy Gradients to work better than Q Learning when tuned well.
连DQN的作者都承认,PG比DQL表现得更好。😝
Pong 为例
我们以雅达利2600上的游戏Pong为例,来展示算法的思想和细节。

Pong就是一个类似于乒乓的游戏,你要控制右边的板子,把左边电脑控制的板子打过来的球打过去,对方没接到你得一分,你没接到对方就得一分。把这个游戏拆分成计算机能够懂得的模型,就是:我们看到一帧图片(比如说210*160*3的像素),通过分析图片中板子和球的位置和运动趋势,来做出板子移动的决策,这个决策只有两个:上(UP)和下(DOWN)。
Policy Network
首先我们要定义一个决策网络(Policy Network)。这个网络会收到游戏的状态,然后输出在这个状态下应该做的决策。在Pong中,我们的输入是一帧图片,输出是UP or DOWN,因为只有两个行为,所以我们可以只用一个神经元就能表示了(当然也可以用两个,如果用一个,那么输出其实是做出UP或者DOWN策略的概率)。
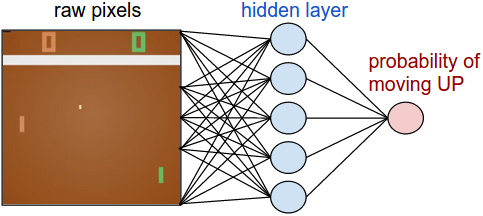
这是我们的计算代码:
1 | h = np.dot(W1, x) # compute hidden layer neuron activations |
直观上来说,隐层(W1)提取了图片中的各个特征,比如板子在哪儿,球在哪儿,输出层(W2)则决定了UP和DOWN的概率,所以,在Policy Network中,W1和W2是最重要的参数,我们要训练的就是这两组参数。
一般来说,我们会用至少两帧图片作为输入(把两帧图加起来或者减一下,或者干脆并排放在一起),为了使神经网络能够识别出连续的动作。
疑问:Policy Network抽象上来说,实际上就是根据一帧帧的图像来反馈相对应的一个个动作,问题在于,也许我到第20个动作才得分,但是我之所以能得分,是取决于我第10个动作精妙的技巧,但是Policy Network肯定不知道啊,那么我们又谈何学习这个动作,增加这个动作的概率呢?所以问题在于,我们要知道是哪一个动作决定了我得分,并且在我知道这个得分后学习到了这个动作。
Supervised Learning
如果你之前接触过监督学习,就会发现决策网络和监督学习是非常像的,唯一一点不同就是Label,那么我们在学习Policy Gradient之前,就先谈谈监督学习(Supervised Learning)。
如下图,我们输入一张图片,得到了输出,输出的是log概率(是log概率还是原始概率,不是关键)。在监督学习下,我们知道在这种情况下应该怎么做,假设我们知道应该UP,那么我们就可以用BP算法来更新权重,来达到增加在这种情况下得出UP决策的概率。
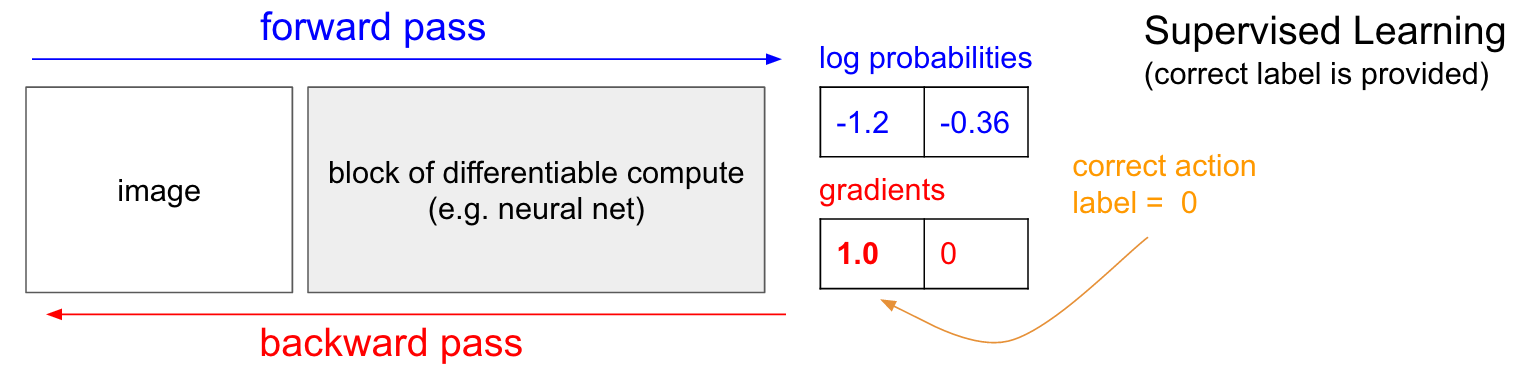
关于监督学习的内容不再赘述,可以查相关资料。
Policy Gradient
那么如果我们没有Label怎么办呢?假如我们进行了一次计算,得到UP的概率为30%,DOWN的概率为70%,那么我们就会在这个分布中随机选择一个,假如选中的是DOWN吧,那么在这时就让板子往下移动,如果这个移动是好的,那么Label就是positive的,在backprop后就增加在这个状态下DOWN的概率。问题是,我们怎么知道这就是好的呢?比如我在第一帧选择了DOWN,然后在20帧才赢/输了游戏,我又不知道第一帧的动作对结果有什么影响。
我们可以这么做,先做一系列动作,直到游戏结束,然后再根据结果,对这一串动作中的每一个动作标记Label。比如说我第一帧DOWN,然后最后赢了,那么DOWN的Label就是positive的。
在PG中,我们的损失函数是$\sum_iA_ilogp(y_i|x_i)$,其中$A_i$是advantage,如果赢了就是1,输了就是-1;$y_i$是我们选取的动作;$x_i$是输入的状态(在Pong例子中是图片(像素))。
以上以pong为例,对advantag的选择也过于草率(因为一律都是1或者0),实际上,对于不同的动作$x$,advange是不同的。
下面我们抛去pong这个例子,来重新描述policy gradient。
基本组件
对于一个强化学习问题,我们首先要明确,这个问题的基本对象有这些:Actor、Environment、Reward Function。
举个例子,AlphaGo下围棋的问题,Actor是AlphaGo,Environment是对手和棋盘,Reward Function基于围棋的规则。再举个栗子,我们玩电子游戏,手柄是Actor,电脑屏幕或者游戏机是Environment,Reward Function是杀死敌人或者占领据点(还是依据游戏规则)。其中Environment和Reward Function是我们无法在训练过程中改变的,只有Actor是受控的。
那么如何控制Actor?
Policy of Actor
我们对Actor的控制,需要策略,而策略我们用 $\pi$ 符号表示。
$\pi$ 是一个参数为 $\theta$ 的神经网络,输入是observation(矩阵);输出是数量为 $n$ 的神经元。
observation是给神经网络提供当前状态的参数,我们可以把游戏的当前图像作为observation,这时observation实际上是一串像素,我们也可以直接把各种参数作为observation,比如说我和敌人的距离、我方英雄技能的攻击范围。总之,observation提供了当前状态的特征。
输出的每个神经元代表一个动作,神经元包含的值表示这个动作的发生概率。
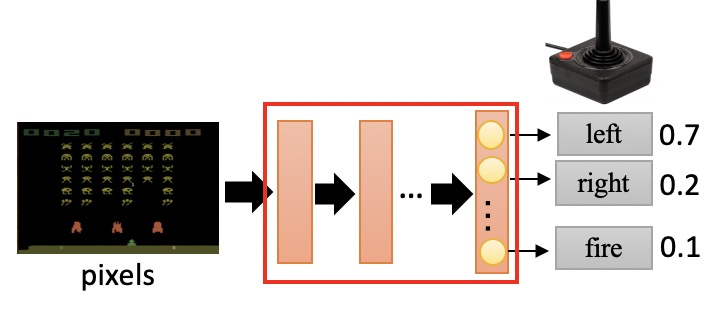
我们会选择概率最高的动作,作为策略的最终结果,然后根据反馈,计算这个动作的得分reward,第$i$个动作$a_i$的reward用$r_i$表示。
以电脑游戏为例
比如说我们玩一个电脑游戏,游戏现在的状态是$s_1$,然后 $\pi$ 选择了动作$a_1$,游戏照做了,然后我们计算一个reward $r_1$;游戏在执行了动作$a_1$后的状态为$s_2$,然后我们再选择了动作$a_2$,执行动作后,计算了一个reward $r_2$,这样一直下去,直到游戏结束(游戏赢了或者输了)。
截止游戏结束,我们一共选择了$T$个动作,计算出了$T$个reward,这一回合我们称之为一个episode,一个episode的整个reward是每个动作的reward之和:
$R = \sum^T_{t=1}{r_t}$
我们用一个图来更直观地看看在这个过程中Actor, Environment, Reward 之间的关系。
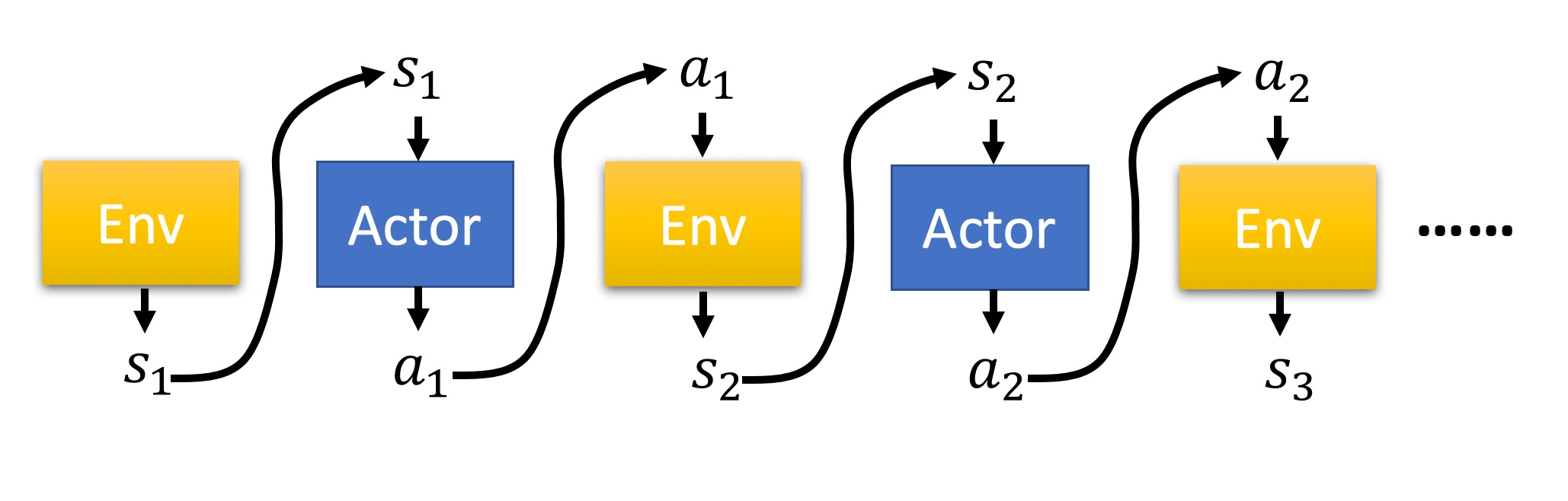
这整个episode是Environment、Actor之间的交互,在episode中产生了一串环境与动作的序列,叫做Trajectory
Trajectory $\tau = {s_1,a_1,s_2,a_2,…,s_T,a_T}$
我们可以算出整个trajectory的概率$p_\theta(\tau)$
$p_\theta(\tau)=p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)p_\theta(a_2|s_2)…=p(s_1)\Pi^T_{t=1}p_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)$
有一点很重要,虽然在episode中,$\theta $是确定的,但是Environment是不受我们控制的,所以即使在相同的$\theta$下,游戏状态$s_i$是不受控的,所以在不同的状态下,产生出的trajectory也会不同。所以要求在 $\theta$ 下的Reward,我们需要求R的期望Expectation
$\overline{R_\theta}=\sum_\tau{R(\tau)p_\theta{(\tau)}=E_{\tau{-}{p_\theta}}[R(\tau)]}$
我们的目的很明确很简单,就是调整$\theta$把$\overline{R_\theta}$最大化,下面就是我们常用的梯度下降(Gradient Descent)
$\theta \leftarrow \theta + {\eta} {\nabla} \overline{R_{\theta}}$
其中
$\nabla\overline{R_\theta}=\sum_\tau{R(\tau){\nabla}p_\theta{(\tau)}}=E_{\tau{-}{p_\theta}}[R(\tau){\nabla}logp_{\theta}(\tau)]$
${\approx}\frac{1}{N}\sum^N_{n=1}R(\tau^n){\nabla}logp_{\theta}(\tau^n)$
$=\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}R(\tau^n){\nabla}logp_{\theta}(a^n_t|s^n_t)$
整个过程如图
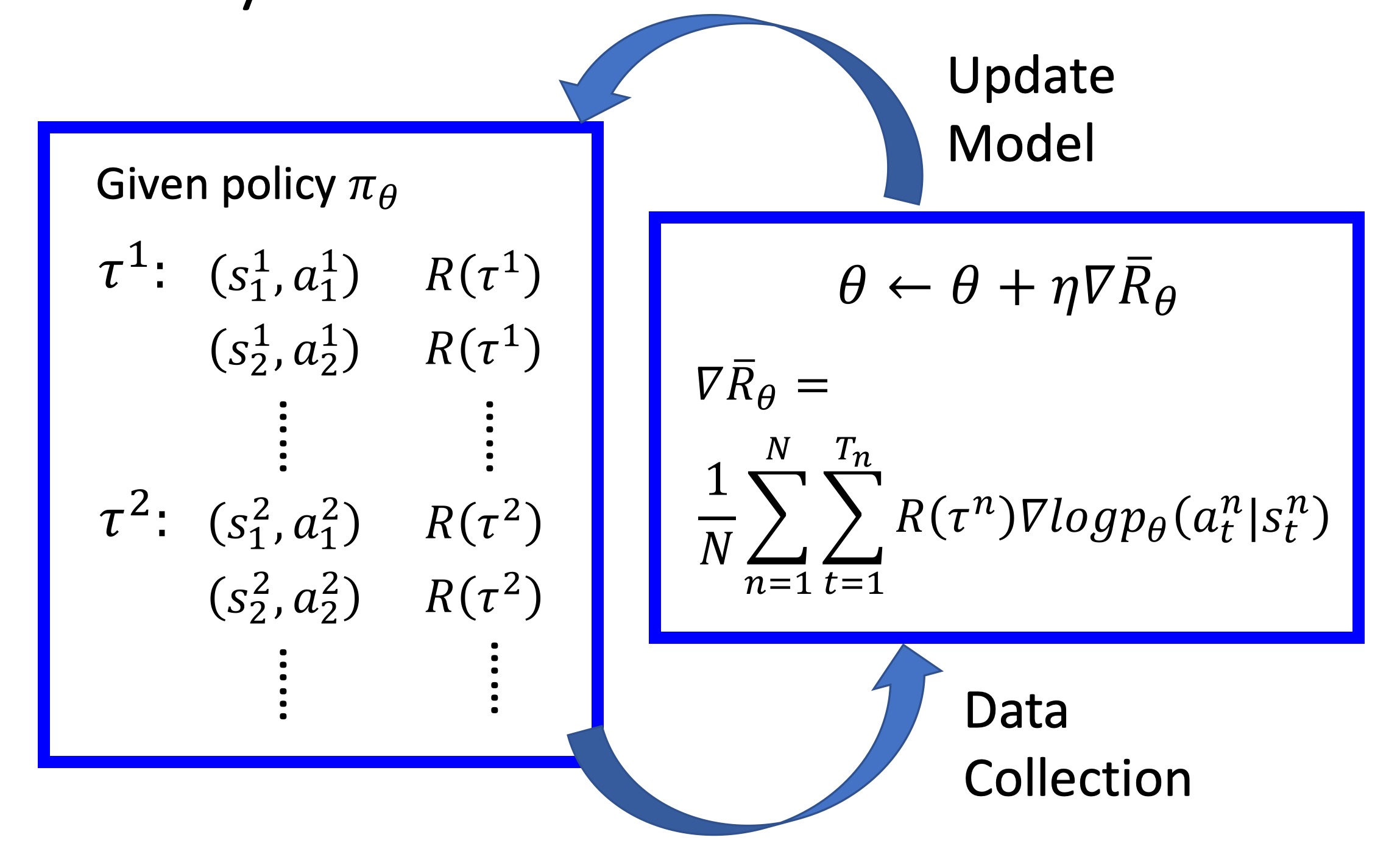
在$N$个episode中,我们要记录每一个$\tau^n$中的序列对$(s^n_i,a^n_i)$,记录$\tau^n$的reward$R({\tau}^n)$,然后对$\theta$进行更新。
Important Tips
在Policy Gradient中,我们可以做一些优化,这些优化包括:增加基线、分配合适奖励值
Tip1: Add a Baseline
增加基线,很好理解,我们看下面这个情况:
在Policy Gradient中,我们常常会发现在实际情况下,每一个动作的奖励值都是正的,比如说我们训练Agent玩FIFA,因为Agent进的球最少是0,其奖励值不可能是一个负数。
但是实际上,即使都是正的,也不会影响到我们训练的结果,因为奖励值有多有少,所以在回馈的时候,对参数的调整也有大有小。奖励值大的,参数就往这一个动作序列靠近得大;奖励值小的,参数就往这一个动作序列靠近得小。因为输出的动作是根据动作的概率来判定的,而所有的动作概率之和为1,一个动作概率大了,其他动作的概率就会变小,所以参数倾向于对奖励值大的动作靠近,实际上就是在远离奖励值较小的动作。
但问题是,注意我们之前推导的梯度下降公式:
$\nabla\overline{R_\theta}{\approx}\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}R(\tau^n){\nabla}logp_{\theta}(a^n_t|s^n_t)$
我们是在对动作序列 $\tau^{i}$ 进行采样,采样的结果是,我们不可能把所有的可能序列都采集到。所以会出现这种情况:有一个动作序列${\tau}^{j}$的奖励值是很高的,但是我们没有采样到,我们只采样到了不是很高的动作序列。那么我们就只能在这一群矮子中挑高的,把参数调整得靠近其中最高的动作序列,提高一个序列几率代表着减少其他动作序列的几率,所以那个原本奖励值最高的${\tau}^{j}$,就被埋没了。气不气?
所以我们提出,加一条基线,这样矮子就不会因为运气好,没和高子排在一起而被当成高子处理了。加一条基线,在公式中表示为奖励值多减了一个$b$:
$\nabla\overline{R_\theta}{\approx}\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}(R(\tau^n)-b){\nabla}logp_{\theta}(a^n_t|s^n_t)$
其中这个$b$,我们一般取所有序列总奖励值的期望:
$b {\approx}E[R({\tau})]$
Tip2: Assign Suitable Credit
我们看下面这个例子:
我有两个episode:

根据公式
$\nabla\overline{R_\theta}{\approx}\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}(R(\tau^n)-b){\nabla}logp_{\theta}(a^n_t|s^n_t)$
我们要对每一个Action都乘上相同的R,在episode1中是3,episode2中,是7。
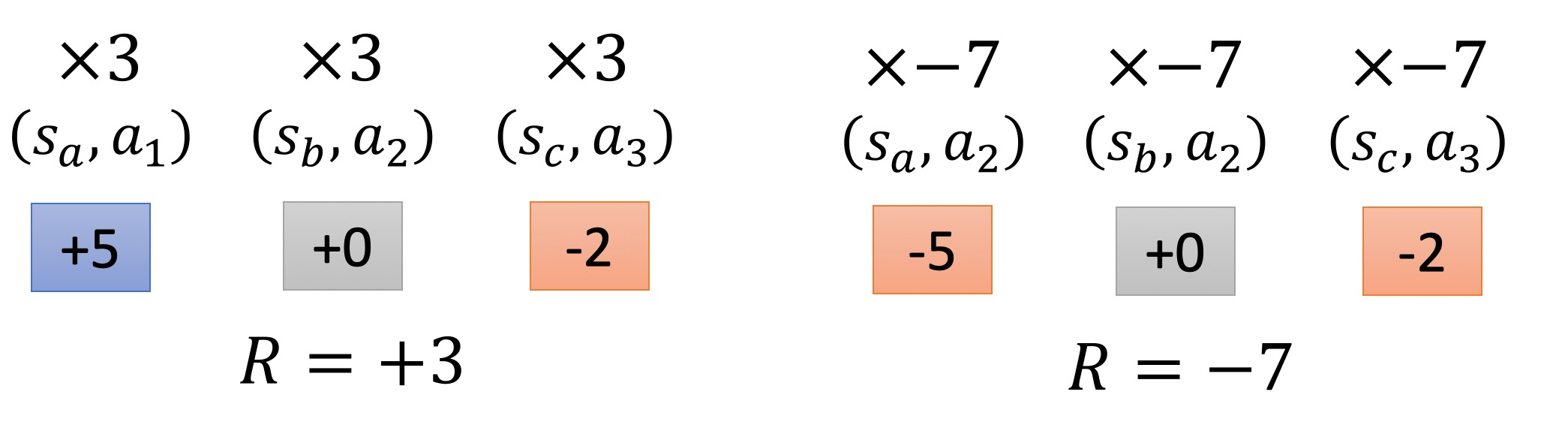
很显然,这是很不公平的。因为在最终结果好的episode里,指不准有一个action是不好的。比如说上图的episode1,它的action2导致了后来action3的得分为负。但是我们同样把它看成了一个好的动作,并且增大了这个动作的几率。
同样的,即使在结果不好的episode里,也可能有好的action。比如说上图的episode2,它的action2虽然导致了后来action3的得分也为负,但是负的程度变小了,说明action2还是有益的。
那么我们可以把代替原来的公式:
$\nabla\overline{R_\theta}{\approx}\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}(R(\tau^n)-b){\nabla}logp_{\theta}(a^n_t|s^n_t)$
代替为以下公式:
$\nabla\overline{R_\theta}{\approx}\frac{1}{N}\sum^N_{n=1}\sum^{T_n}_{t=1}({\sum_{t’=t}^{T_n}r_{t’}^{n}}-b){\nabla}logp_{\theta}(a^n_t|s^n_t)$
其中,我们把
$R(\tau^n)$
替换成了
${\sum_{t’=t}^{T_n}r_{t’}^{n}}$
什么意思呢?我们由原来的,对动作${a_i}$都乘上一个相同的R,变成乘上一个以动作$a_i$为起点的动作序列的奖励值。直观上理解,就是对每个动作的调节,不再是看整个动作序列的结果了,而是看这个动作在整个动作序列中发挥的作用。
理解了上面的意思,我们可以进一步优化,将
${\sum_{t’=t}^{T_n}r_{t’}^{n}}$
改进为
${\sum_{t’=t}^{T_n}{\gamma}^{t’-t}r_{t’}^{n}}$
其中$0<{\gamma}<1$
这个也很好理解,随着动作$a_i$和$a_j$之前隔的时间越来越久,两个动作的相关性就越来越小。
Reference:
Deep Reinforcement Learning: Pong from Pixels
http://karpathy.github.io/2016/05/31/rl/
Reinforcement learning An introduction
Policy gradient methods for reinforcement learning with function approximation.
“Deep Reinforcement Learning, 2018” by 李宏毅
- 本文作者: YA
- 本文链接: https://shiyuang-scu.github.io/2018/11/03/Policy-Gradient/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!


