整个统计机器学习模型选择的逻辑，在我看来，其实是：

1. 模型测试：通过某种方法（留出法、交叉验证法……），使模型输出一系列数据，这个数据是其性能的表现；
2. 性能度量：根据模型展示出的一系列数据，运用数学方法对数据进行处理，使得处理后的数据能够直观地代表模型的性能；(就是问题一讨论的内容)
3. 模型评估：对由第二步处理后的数据进行比较，每个模型都有自己的性能度量数据，我们将每个模型的性能度量数据进行比较，这个比较不是单纯的比大小，需要运用数学方法对每个模型的性能度量数据进行处理，在处理完后得到的数据，才能进行比较；
4. 模型选择：根据比较的结果，选择最好的模型。

每个步骤的名称是我自己定的，肯定和经典书籍中的描述有所出入，整个流程的逻辑应该是清楚的。

本文简述了模型评估与选择的第1步和第2步，具体地说，本文解决了两个问题：

1. 怎样进行模型测试；
2. 如何得到一个模型的性能度量。

How to evaluate the performance of a model?

性能度量(Performance measure)，字面理解就是对学习模型性能的度量，那什么叫做模型的性能呢？简单来说，就是度量模型的泛化能力。性能度量的目的，是通过对模型的性能评估，来帮助决策——选择哪一种模型、选择哪一个参数、选择什么优化方法。

在预测任务中，给定样例集$D={(x_1,y_1),(x_2,y_2),…(x_m,y_m)}$，其中$y_i$是示例$x_i$的真实标记。要评估学习器$f$的性能，就要把学习器的预测结果$f(x)$与真实标记$y$进行比较。

（这里把学习器的预测结果，用$f(x)$符号表示，表明了一个思想：所谓模型，实际上就是一个映射或者函数，把一个$x$映射到$y$上。）

在分类任务中，有以下常用的性能度量。

错误率与精度

这个很容易理解，错误率就是模型在测试集中，分类错误的样本数占样本总数的比例，精度就是分类正确的样本数占总样本数的比例。

数学一点，可以用以下公式表示错误率

$$E(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}{i}\right) \neq y{i}\right)$$

用以下公式表示精度

$$\begin{aligned} \operatorname{acc}(f ; D) &=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}{i}\right)=y{i}\right) \ &=1-E(f ; D) \end{aligned}$$

查准率、查全率与$F_{\beta}$

为什么选择查准率与查全率

很多情况下，我只评估错误率与精度是不够的。

举个例子，在医疗诊断上，分类模型对病人是否患病的判断，要求宁可判成阳性(患病)，也不能判成阴性，因为错判成阴性的后果会比错判成阳性的后果更加严重。这时，我们关心的是”判断患病的人在真正患病的人中比例是多少”，而不是”在所有判断中，正确判断占所有判断的比例”。我们不在乎整体的精度、不在乎判断得病但是没得病的比例有多少——这个错判带来的后果比较小。我们只在乎判断患病的部分是否有较高的精度。

什么是查准率与查全率

我们引入一个概念，”混淆矩阵”(Confusion Matrix)。

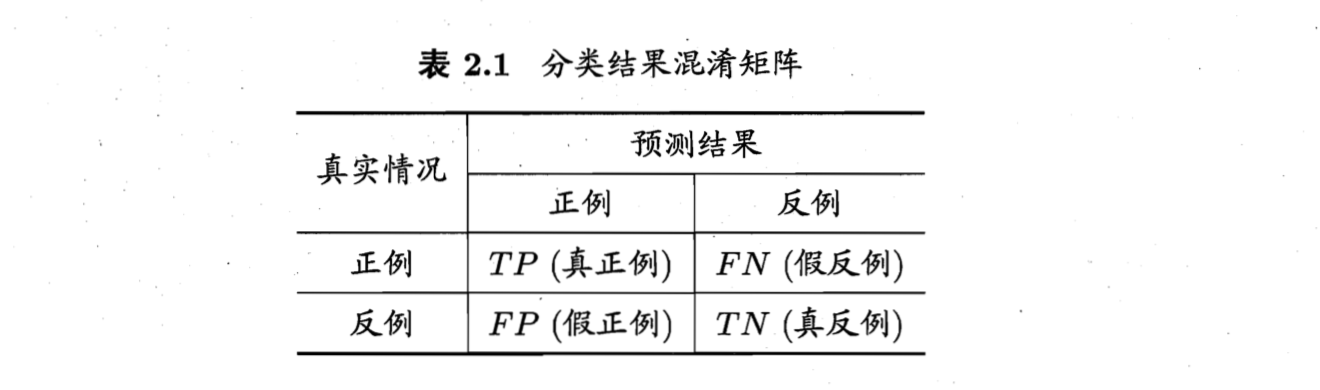
如图，实际上分类器的预测结果有四种情况：真阳性（true positive）、假阳性（false positive）、真阴性（true negative）、假阴性(false negative)。

那么，所谓的查准率P和查全率R，就可以定义为

$$P=\frac{T P}{T P+F P}$$

$$R=\frac{T P}{T P+F N}$$

仔细想想，其实查准率P和查全率R，在很多情况下是互斥的：查准率高的时候，查全率往往低；查准率低的时候，查全率往往高。

举个例子吧，我想要把真的患病的人尽可能多地查出来，那么只要我增加判断得病的人的数量。极端一点，我把所有人都标记成患病，那么的确患病的人都被标记了，查全率就是100%，但查准率就很低了。

同样的，如果我要尽可能精确地查出患病的人，那么宁可放过不可错杀，这样就难免放过部分真的患病的人，虽然这时候查准率高了，但是查全率就低了。

如何根据查准率与查全率选择模型

这一部分涉及到了问题二(什么是模型选择、如何选择模型)，为了内容的完整性，就在问题一中阐述了。

分类器对测试数据集输出一系列为正样本的概率，根据概率由大到小排列，然后从前到后选择样本，作为一个判断是否是正样本的阈值，若大于该阈值，则为正样本；反之则为负样本。

每次阈值的设置都有对应的查准率和查全率，因此以查全率为横坐标，查准率为纵坐标，就可以得到查准率-查全率曲线，就是“P-R曲线”。

如图所示，

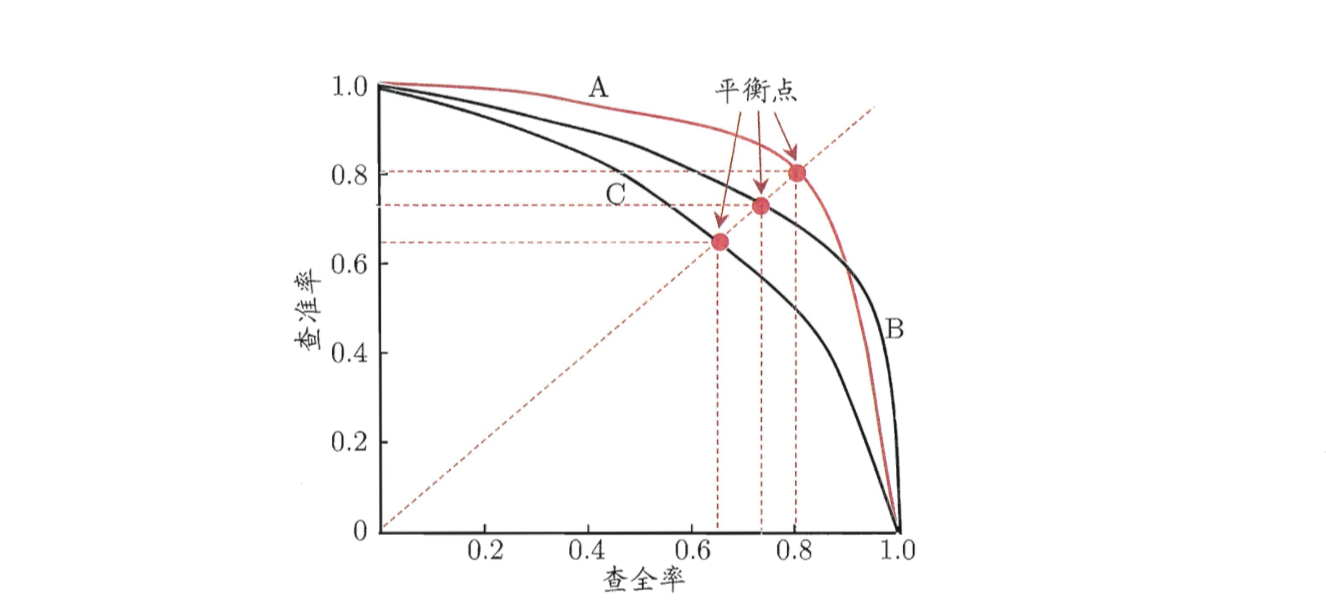
形象地说，如果一个模型A的P-R曲线把另一个模型B的曲线包住了，那么A就比B好。这个很好理解，看图就行了。

如果两个模型的曲线有交点，那么直观上其实分不出好坏，比较直接的方法就是比曲线围成的面积谁大。

然而算面积太麻烦了，也太慢了，所以又有一个简单的度量方法：”平衡点”(Break-Event Point)。这个平衡点，就是当P=R，也就是查准率等于查全率的时候的取值。平衡点越大，说明模型越好。

然而平衡点也太简单了，无法很好地表达更详细的需求和度量。比如说，我希望查准率要更高一点，查全率没关系，那么平衡点和面积就没用了。

因此出现了$F_{\beta}$度量，如下公示所述

$$F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R}$$

当$\beta \le 1$时，P（查准率）对$F_{\beta}$的影响更大，当$\beta \ge 1$时，R（查全率）的影响更大。这个可以自己算一下，不解释了。

ROC与AUC

ROC是受试者工作特征(Receiver Operating Characteristic)的简称，这个概念和P-R曲线很像，就是分类器对测试数据集输出一系列为正样本的概率，根据概率由大到小排列，然后从前到后选择样本，作为一个判断是否是正样本的阈值，若大于该阈值，则为正样本；反之则为负样本。

但是坐标轴表示的量不一样，ROC的纵坐标轴是”真阳性率”(True Positive Rate TPR)，横坐标轴是”假阳性率”(False Positive Rate FPR)。

数学表示为

$$\mathrm{TPR}=\frac{T P}{T P+F N}$$

$$\mathrm{FPR}=\frac{F P}{T N+F P}$$

如图，这就是ROC曲线

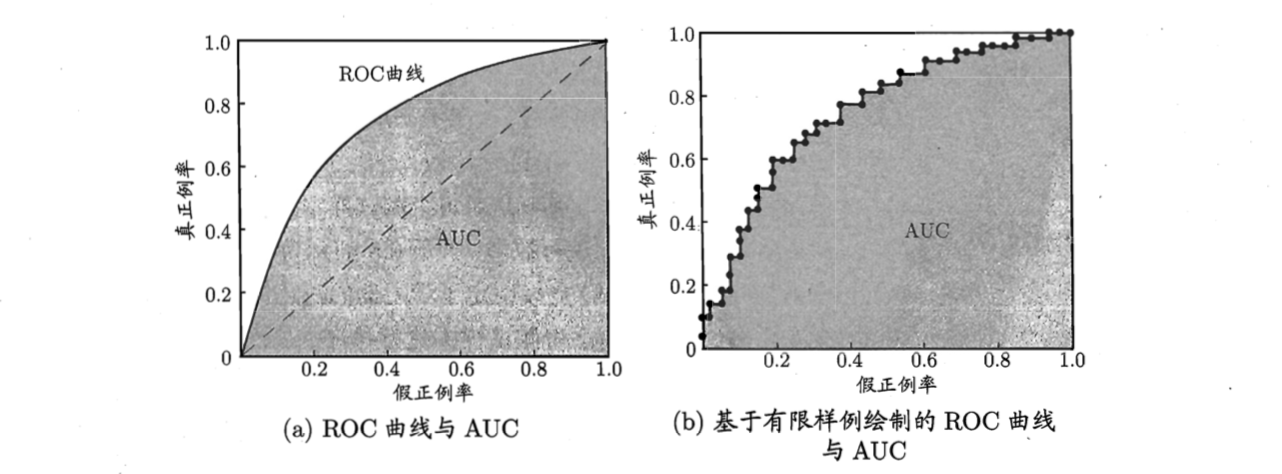
比较模型的好坏，还是根据哪个包住了哪个，如果两个曲线交叉，那么就看曲线围成的面积，这个面积有姓名：AUC (Area Under ROC Curve)。(为什么P-R曲线的面积没有名字呢？也许可以叫AUPRC……)

What is model selection? How to solve this issue?

问题一解决了如何度量模型的问题，问题二需要我们解决的事如何选择模型的问题。

为什么要选择模型？因为机器学习的模型有很多，在分类问题上，有线性回归、逻辑回归、神经网络、KNN等模型。相同的算法，不同的模型，结果也可能是千差万别的。

如何度量模型的性能，在问题一中已经说明了，但是接下来的问题就是，用什么方法去使得模型能够显示出自己的性能好坏。

整个模型选择的逻辑，在我看来，其实是：

1. 模型测试：通过某种方法（留出法、交叉验证法……），使模型输出一系列数据，这个数据是其性能的表现；
2. 性能度量：根据模型展示出的一系列数据，运用数学方法对数据进行处理，使得处理后的数据能够直观地代表模型的性能；(就是问题一讨论的内容)
3. 模型评估：对由第二步处理后的数据进行比较，每个模型都有自己的性能度量数据，我们将每个模型的性能度量数据进行比较，这个比较不是单纯的比大小，需要运用数学方法对每个模型的性能度量数据进行处理，在处理完后得到的数据，才能进行比较。
4. 模型选择：根据比较的结果，选择最好的模型。

每个步骤的名称是我自己定的，肯定和经典书籍中的描述有所出入，但是整个流程的逻辑应该是对的。

下面简单阐述第一步，模型测试。

首先，统计机器学习的最基本的基础概念是，独立同分布。因为统计机器学习方法是与统计密切相关的，极度依赖数据，所以数据的质量直接决定了训练模型的质量，trash in trash out。

独立同分布就是一个数据集最基本的应该具有的性质，如果不满足独立同分布，那么这个数据集就是有所偏袒的，数据在某一个地方集中分布，在另一个地方很稀疏，训练的模型泛化能力肯定不好。尽可能采样更多的数据，是解决非独立同分布又暴力又简单的方法。

下面要介绍的几种方法，将数据集分为两个部分，一个部分进行训练，一个部分进行测试，之所以能够这样做，就是基于独立同分布这个假设。

留出法

“留出法“(hold-out)，简单地说就是将数据集 $D$ 划分成两个互斥的集合，一个集合作为训练集 $S$ ，一个集合作为测试集 $T$。在 $S$ 上训练，在$T$上评估，一般训练集与测试集的大小比是2：1。

问题来了，为了保持数据的独立同分布，我们要做的是尽可能完美地使划分出来的训练集和测试集数据，保持原有数据分布的一致性，避免因为数据划分过程中某些额外引入的偏差，导致训练结果、测试结果出现问题。

划分过程中存在很多的变量，不能保证达到分布一致性。我们有很多因素需要考虑：按什么比例划分训练集和测试集，在训练集和测试集中应该包含怎么样的数据。

比如一个分类问题，我有1000个数据，按2：1的大小比划分训练集与测试集，那么在训练集中该划多少个正例和反例到训练集和测试集？又因为每一个正例反例的特征不同，对模型训练的影响也非常大，比如我有一堆正例集中在一个圈内，圈外又有稀稀疏疏的一些正例，那么我把圈外那些稀疏的正例划进训练集，训练结果一定非常差。同理，如果划进测试集内，测试结果也肯定非常差。

所以，为了尽量减少这种误差，我们能做的就是进行若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。举例来说，我进行一百次划分一百次实验评估，然后对这一百个评估数据取平均值作为最终评估结果。

交叉验证法

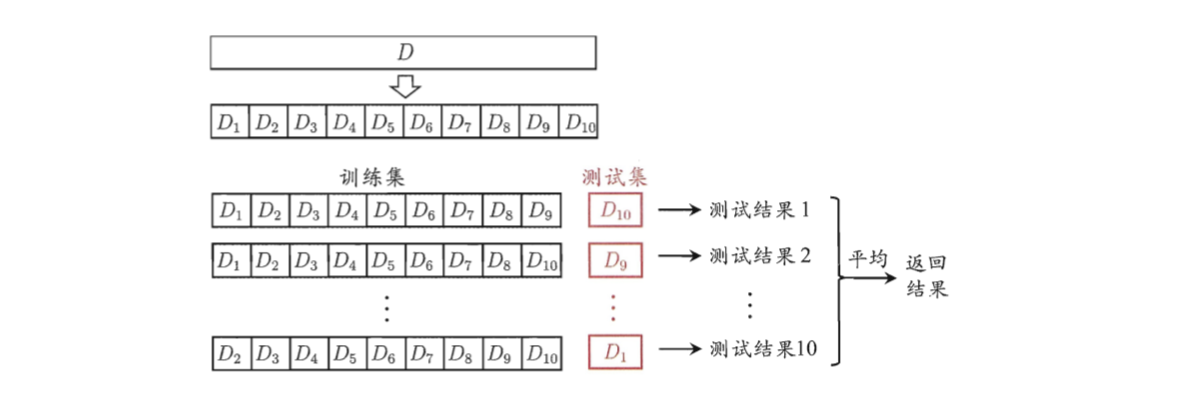
“交叉验证法”(cross validation)将数据集 $D$ 划分成 $k$ 个大小相似的互斥子集，每次用 $k-1$ 个子集的并集作为训练集，余下的子集作为测试集，这样就能进行 $k$ 次训练和测试，最后取结果的平均值。 因为交叉验证法与 $k$ 关系密切，所以为了强调 $k$ ，也会将交叉验证法称作”k折交叉验证”(k-fold cross validation)。

一般来说，会把 $k$ 取成10，如下图就是10折交叉验证的示意图。

留一法

有一种方法，作为交叉验证法的特例，可以很好地使得训练模型反应数据集的分布规律，就是”留一法“(Leave-One-Out LOO)。

假定数据集 $D$ 有 $m$ 个样本，若令 $k=m$，相当于把每一个数据划成一个单独的组，那么需要进行$m$次训练。这个方法得到的模型和评估结果都相对更准确，但是问题是计算量非常非常大，我们知道一般数据集都是非常庞大的，几百万的数据集都算是小数据集了，想想要进行数百万的训练和测试，还不包括调参。

自助法

以上我们可以看到，我们将数据集 $D$ 分成训练集 $S$ 和测试集 $T$ ，需要考虑两部分的大小，训练集和测试集不能太大也不能太小，这对于数据集很小的情况简直是噩梦。我只有100个数据，再划分成70个数据的训练集，得到的模型性能很大可能会很差。所以需要解决的是减少训练样本规模不同造成的影响。

“自助法”(bootstrapping)是一个不错的解决方案。具体方法是：一个有$m$个数据的数据集$D$，我们对它进行采样，产生数据集$D’$。采样方法就是，每次随机从$D$中选择一个样本复制进$D’$，同时仍保留这个数据在$D$中。把这个过程重复$m$次，就得到了一个包含$m$个数据的数据集$D’$。

当然，$D’$ 中肯定有部分样本重复出现，有部分样本从没出现，我们做一个简单的估计，一个样本在$m$次采样中不被采到的概率为$\left(1-\frac{1}{m}\right)^{m}$取极限就是

$$\lim _{m \rightarrow \infty}\left(1-\frac{1}{m}\right)^{m} \mapsto \frac{1}{e} \approx 0.368$$

所以，理想情况下，在$D$中有大约36.8%的数据没出现在$D’$中，也就是大约三分之一。

我们就可以将$D’$作为训练集，$\frac{D} {D’}$作为测试集。如此，实际训练得到的模型和期望训练得到的模型都使用$m$个训练样本，同时仍有大约三分之一的没在训练集中出现的样本作为测试集。

调参

我们选定了一个模型，这个模型通常有许多参数需要设定，对于一个模型来说，其参数可以分为普通参数和超参数。

在不引入强化学习的前提下，普通参数是可以被梯度下降所更新的，也就是训练集所更新的参数。另外，还有超参数的概念，比如网络层数、网络节点数、迭代次数、学习率等等，这些参数不在梯度下降的更新范围内。而超参数就需要人工设定，这就是”调参”(parameter tuning)。

我们一般调参的做法是，对每个参数设定一个范围和步长，例如我在$[0,0.2]$范围内选择0.05作为步长，那么待定参数就有5个，我通过训练模型评估模型，来选择一个最优的参数。当然，这样离散的参数选择，得到的参数肯定不是最优解，只是作为一个近似解。此外，时间开销也非常大，想一想，如果有3个参数，每个参数有5个待定值，那么就需要训练测试125个模型来评估，这仅仅是3个参数带来的计算量，而在企业级的深度神经网络中，往往有上百亿个参数。

在这里，我们要注意区分训练集、测试集、验证集。简单地说，训练集和验证集进行了对模型参数的调整，前者调整了普通参数，后者调整超参数。而训练集就是在模型训练好之后，对模型进行性能度量，没有参与训练。

从狭义来讲，验证集没有参与梯度下降的过程，也就是说是没有经过训练的；但从广义上来看，验证集却参与了一个“人工调参”的过程，我们根据验证集的结果调节了迭代数、调节了学习率等等，使得结果在验证集上最优。因此，我们也可以认为，验证集也参与了训练。

那么就很明显了，我们还需要一个完全没有经过训练的集合，那就是测试集，我们既不用测试集梯度下降，也不用它来控制超参数，只是在模型最终训练完成后，用来测试一下最后准确率。

Reference

• 问题一（如何评估分类器的性能）参照了
  • 西瓜书（周志华《机器学习》）的第二章模型评估与选择
  • 小蓝书（李航《统计学习方法》）第一章第四节模型评估和模型选择

在学习了相关概念后，进行了自己的阐述和总结。

• 问题二(什么是模型选择、如何选择模型)参照了

  • 林轩田机器学习基石课程的Validation部分

  • 西瓜书（周志华《机器学习》）的第二章模型评估与选择

同样的，问题的解答是在理解知识的基础上，进行自己的阐述。