本文简单介绍了感知机(Perceptron)与支持向量机(Support Vector Machine SVM)的部分概念。
本文没有系统地介绍两种算法,只是作为四川大学彭玺老师《机器学习引论》的课程作业和笔记,以供参考。
机器学习中有一个概念叫做『线性可分』,意思是可以画一条线把把两个不同的类别分开,比方说男左女右排好队,就是线性可分的。不过有的时候大家混在一起乱成一锅粥,完全没有办法找到这么一条线,这时候怎么办呢?也有办法,就是不通过当前的角度来看问题,把问题投射到更高维的空间去,就可能在更高维的空间里找到新的『线性可分』。
The evolution of neuron from biology to mathematics?
1890:美国心理学家和哲学家William James在其著作中指出——当两个事件同时发生时,涉及到的大脑过程间的连接将会增强,这是无监督的Hebb学习规则的灵感来源。此外,James还提出了加权(weighted)、可变(modifiable) 、及并行连接(parallel connections)等神经网络至今采用的基本概念。
1906:神经科学家、诺贝尔奖得主S. R. Cajal对神经元突触的可变的连接方式的发现为神经元建模提供了基本模型。
1932:James的学生Edward Lee Thorndike被认为是第一位真正的连接主义者。其专著《The Fundamentals of Learning》中提出学习是刺激和响应之间建立关联的结果。y?=f(x)
1943:C. L. Hull则提出神经元的输出是其输入与其他多个传入脉冲叠加的非线性函数,学习 是对神经元连接的修改。y=f(Wx) 这一理论是神经元连接模型、激活状态和学习算法的生理学依据。此外,Hull还提出了几个经验性的公式,其本质上就是Bernard Widrow和Marcian Hoff提出的Delta rule。
1943:Warren McCulloch和Walter Pitts提出第一个人工神经元模型——M-P模型,其通过阈值加权和定义了输入与输出的关系,奠定了人工神经元的数学模型基础。此外,McCulloch和Pitts 于1947年的工作是模式识别领域的开端; y=f(Wx+b)
1957:基于上述发现和研究,Frank Rosenblatt发明了Perceptron,是第一个2层的ANN,同时也是第一个基于学习的能处理线性可分数据的分类器。
The key concepts of Perceptron and its limitations.
Key Concepts
感知机(perceptron)由两层神经元组成,输入层接受外界输入信号,传递给输出层,输出层是M-P神经元,也称为”阈值逻辑单元”(threshold logic unit)。
因此,感知机具有M-P神经元的特点,输入信号通过带权重的连接进行传递,通过”激活函数”处理以产生神经元的输出,给定训练数据集,权重$w$可通过学习得到。其生理学和哲学基础为:
William James:具有加权、可变、并性连接的基本概念;
Edward Lee Thorndike:学习是刺激和响应之间建立关联的结果;
C. L. Hull:神经元的输出是其输入与其他多个传入脉冲叠加的非线性函数,学习是对神经元连接的修改。
感知机与之前的KNN方法相比,更近了一步。
KNN做的是纯粹的”识别”。也就是说,如果用KNN方法,那么我们在一个庞大的数据集下,每次输入一个待分类的数据,都要从头开始做一次计算。举个例子说,我有一大堆兔子和老鼠的图片作为数据集,每张图片都包含着各自所属动物的特征,那么当我拿到一张新的图片,就要拿这张图片与数据集里每一张图片进行比较,哪种动物的图片与这张图片更接近,我们就预测这个图片里是哪种动物。
而perceptron做的是”学习”,它做的不是每次识别、分类都要与每一个数据进行比较,而是作为一种方法,去学习另一种方法,使得通过它学习的这种方法,得到分类结果。本质上,是一个函数的映射过程,感知机需要学习一个函数$f(x)$,只要把待识别的样本$x$放进这个函数里,就会得到一个$y$,这个结果就是$x$的分类结果。
Limitations
- 无最优解
因为感知机的目的是进行分类,通过错误数据,不断调整权重,只要没有错误数据,就不会发生调整。因此,会因为参数初始化、输入训练集的顺序等因素,导致输出的模型,即决策边界千变万化。
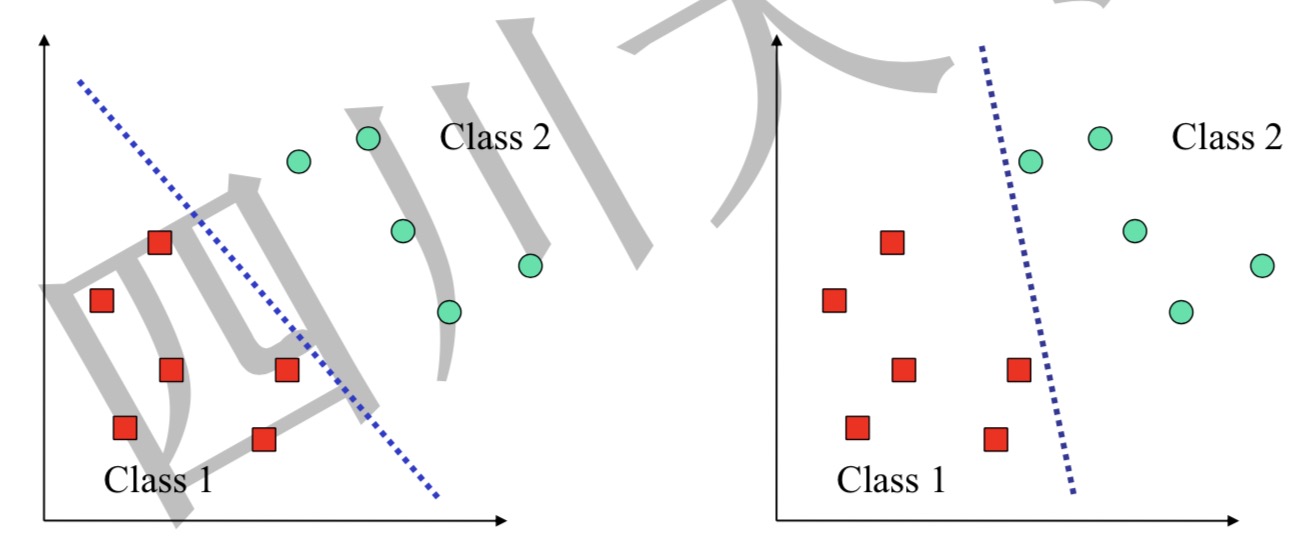
如图,同一个训练集,得到了两个不同的决策边界,那么选择哪一个决策边界?感知机没有给出方法。
- 无法解决非线性可分问题
感知机只有输出层神经元进行激活函数处理,即只有一层功能神经元,所以无法解决非线性可分问题,如异或问题。
Who is Vladimir N. Vapnik.
Vladimir Naumovich Vapnik,1936年12月6日-,俄罗斯统计学家、数学家。他是VC理论(Vapnik Chervonenkis theory)的主要创建人之一。(VC理论是一套机器学习理论,使用统计的方法,因此有别于归纳学习等其它机器学习方法由这套理论所引出的支持向量机对机器学习的理论界以及各个应用领域都有极大的贡献。)
Vapnik出生于苏联。1958年,他在撒马尔罕(现属乌兹别克斯坦)的乌兹别克国立大学完成了硕士学业。1964年,他于莫斯科的控制科学学院获得博士学位。毕业后,他一直在该校工作直到1990年,在此期间,他成为了该校计算机科学与研究系的系主任。
1995年,他被伦敦大学聘为计算机与统计科学专业的教授。1991至2001年间,他工作于AT&T贝尔实验室(后来的香农实验室),并和他的同事们一起发明了支持向量机理论。他们为机器学习的许多方法奠定了理论基础。
现在,他工作于新泽西州普林斯顿的NEC实验室。他同时是哥伦比亚大学的特聘教授。
2006年,他成为美国国家工程院院士。
Maximum Margin Principle and why support vector is important?
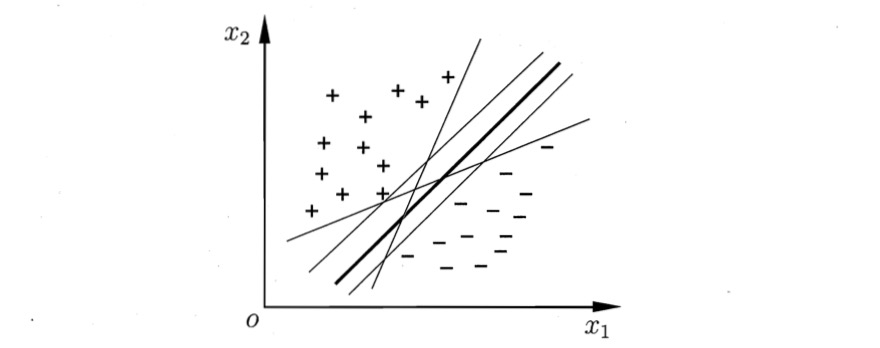
Maximum Margin Principle
接着上面一个问题,感知机有一个问题,就是无法找到一个最优的决策边界,如图,所有的决策边界都能很好地拟合数据集,那么我们应该去找哪一个呢?
直观上看,肯定选择两类样本正中间的决策边界,因为这个决策边界没有偏袒任何一方,很公平地站在两类样本的中间。更准切一点,这个决策边界所产生的分类结果会是拥有泛化能力最强的,鲁棒性最好的。
我们发现,实际上,决策边界应该尽可能远离所有种类的数据样本,这样就会有最好的鲁棒性,我们这个直觉很对,用一条准则来描述我们的直觉,叫最大边界准则(Maximum Margin Principle)。
那么如何利用最大边界准则呢?
最大边界准则,其后包含着一个条件——决策边界尽可能远离所有种类的数据样本,所以,我们需要最大化决策边界与距其最近的数据点的距离$m$,而距离决策边界最近的数据点,就称之为支持向量。
Why support vector is important
支持向量之所以重要,可以从定性和定量两个角度讨论。
定性角度
从定性角度看,最大边界准则或者说SVM的基本概念、原则,就是最大化决策边界与支持向量(support vector)的距离,所以支持向量是整个算法的基础。
定量角度
从定量角度看,支持向量是求出决策边界的重要参数,这一点可以从SVM的数学性质来看。
首先,SVM的思想基础就是,寻找符号最大边界准则的决策边界,假定有一个点$x$,待定决策边界的方程为$w^Tx+b=0$,可得点$x$到待定决策边界的距离$\gamma$为:
$$\gamma=\frac{w^{T} x+b}{|w|}=\frac{f(x)}{|w|}$$
因为$f(x)$作为一个决策边界,当$f(x)>0$时,数据点标签为$y=1$,当$f(x)<0$时,另一边数据点标签为$y=-1$,所以为了防止$\gamma<0$的情况,我们再乘上$y$:
$$\tilde{\gamma}=y \gamma=\frac{\hat{\gamma}}{|w|}$$
最大间隔分类器的目标函数就可以因此定义为:
$$ \max \tilde{\gamma}$$
但同时需要满足条件:
$$y_{i}\left(w^{T} x_{i}+b\right)=\hat{\gamma}_{i} \geq \hat{\gamma}, \quad i=1, \ldots, n$$
为了方便推导和优化,我们可以把$\hat{\gamma}$等于1,这样的处理不会给推导和优化带来任何影响。因此,以上式子就变成了以下形式:
$$\max \frac{1}{|w|}, \quad s . t ., y_{i}\left(w^{T} x_{i}+b\right) \geq 1, i=1, \ldots, n$$
我们可以将以上形式转换成如下形式,之所以这样转换,一方面是为了便于求导,另一方面,求最大值问题和求最小值问题本质上是相同的。
$$\min \frac{1}{2}|w|{^2}, \quad s . t ., y_{i}\left(w^{T} x_{i}+b\right) \geq 1, i=1, \ldots, n$$
我们可以用拉格朗日乘子法解决这个问题。
首先将这个约束形式转换成拉格朗日函数:
$$L(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}|\boldsymbol{w}|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\mathbf{T}} \boldsymbol{x}_{i}+b\right)\right)$$
当某个约束条件不满足时,例如$y_{i}\left(w^{T} x_{i}+b\right) \leq 1$,那么显然有$\theta(w)=\max {\alpha{i} \geq 0} \mathcal{L}(w, b, \alpha)=\infin$。
而当所有约束条件都满足时,则最优值为$\theta(w)=\frac{1}{2}|w|^2$,亦即最初要最小化的量。
所以,我们的目的是最小化$\theta(w)$,也就是:
$$\min _{w, b} \theta(w)=\min _{w, b} \max {\alpha{i} \geq 0} \mathcal{L}(w, b, \alpha)$$
这个求解过程不好做,不妨把最小和最大的位置交换一下,变成:
$$\max {\alpha{i} \geq 0} \min _{w, b} \mathcal{L}(w, b, \alpha)$$
这样的改变满足KKT条件的情况下是没关系的,即要求:
$$\left{\begin{array}{l}{\alpha_{i} \geqslant 0} \ {y_{i} f\left(\boldsymbol{x}{i}\right)-1 \geqslant 0} \ {\alpha{i}\left(y_{i} f\left(\boldsymbol{x}_{i}\right)-1\right)=0}\end{array}\right.$$
注意这组式子,在最后我们还会提到。
为了求解以上式子,我们首先令$\mathcal{L}(w, b, \alpha)$对$w$、$b$求偏导,得到:
$$\boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}$$
$$0=\sum_{i=1}^{m} \alpha_{i} y_{i}$$
将这两个式子代回原式,可得:
$$\max {\alpha} \sum{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}{i}^{\mathrm{T}} \boldsymbol{x}{j}$$
$$\begin{array}{c}{\text {s.t.}, \alpha_{i} \geq 0, i=1, \ldots, n} \ {\sum_{i=1}^{n} \alpha_{i} y=0}\end{array}$$
上式就是原始式的对偶式。这里,我们已经把$w$、$b$消除,只要把每个$\alpha_i$求出,就能求得模型:
$$\begin{aligned} f(\boldsymbol{x}) &=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b \ &=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}+\boldsymbol{b} \end{aligned}$$
从这里我们可以看到为什么支持向量很重要。看我们上面说到的KKT条件,为了满足KKT条件,对于任意的训练样本,总有$\alpha_i=0$或者$y_if(x_i)-1=0$。如果$\alpha_i=0$,那么这个样本点不会在结果中体现;如果$y_if(x_i)-1=0$,那么实际上这个样本点就是支持向量。
通过以上我们可以看到,$w$的训练,是由支持向量决定的。
How to compute the distance between a given data point to the boundary?
点到线的距离公式如下:
$$r=\frac{w^Tx_i+b}{||w||}$$
What limitations the linear SVM suffered from?
线性SVM只能实现线性可分问题,基于训练样本线性可分的假设,即存在一个划分超平面能将训练样本正确分类。
但是现实中,大部分分类任务的原始样本空间内并不存在一个能正确划分两类样本的超平面。
- 本文作者: YA
- 本文链接: https://shiyuang-scu.github.io/2019/04/27/机器学习-感知机与支持向量机/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!


