主成分分析(Principal Component Analysis, PCA)是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

本文从PCA的目的、思想、原理背后的含义出发，试图清晰地解决几个问题：

• 为什么用PCA
• 怎么用PCA
• 为什么这么用PCA

1 问题背景

所谓数据分析，我个人觉得就是在大量数据中找到数据背后隐藏的规律。可以说，机器学习包括深度学习的目的也就在此。

现在我有某个淘宝店2012年全年的流量及交易情况，我想要拿这个数据集来做点事情。这组数据可以看成一组记录的集合，其中每一天的数据是一条记录，格式如下：

(日期, 浏览量, 访客数, 下单数, 成交数, 成交金额)

我们得到一组记录，每条记录可以被表示为一个六维向量，这样的一条五维数据看起来是这个样子的：

$$(2019/2/3, 100, 100, 240, 235, 70000)$$

我们可以拿这个数据集来进行分析，预测在下一个季度该淘宝店的销售额，帮助这家淘宝店决定什么时候多进货。

然而，我们在面对这组数据时，我们会发现，下单数和成交数，概念虽然不一样，但其实差不多，毕竟绝大部分人下单了就不会退了。所以，我们在分析数据时，如果把其中一个去掉，几乎不会影响我们的分析结果。

我们当然可以还是对这一组六维向量进行分析和挖掘，毕竟，下单数和成交数还是不同的概念，表达的信息也有所不同。不过我们知道，很多机器学习算法的复杂度和数据的维数有着密切关系，甚至与维数呈指数级关联。当然，这里区区六维的数据，也许还无所谓，但是实际机器学习中处理成千上万甚至几十万维的情况也并不罕见，在这种情况下，机器学习的资源消耗是不可接受的。

这时候，我介绍一个概念：数据高维导致的维度灾难。

数据的高维导致所谓的维灾 ，本质上是说数据的关键特性主要分布在少量维度(属性)上，其分布于所有维度张成空间的概率接近于0。简单地说，就是真正能看出这组数据规律的重要特性，只集中在个别几个属性上，大部分属性都是没用的，都是一个干扰项。

维度灾难会导致两个问题：

1. 难以得到结论。流行的Euclidean距离平等地对待每一个属性，而不加区分，同时是一种pairwise的距离，故不能真实的描述出数据之间的关系和分布特性。简单地说，因为我们把每一个属性都平等的对待，都平等地进行分析，所以那极少数最能代表数据特征的属性，被淹没在了大量无用的属性中。
2. 时间复杂度极高。不考虑那些没用的属性对我们找出数据规律的影响，就算我们找得到规律，也要花费很大的功夫。因为我们把每一个属性都平等的对待，都平等地进行分析。而分析，就代表着我们要对每一个属性进行计算。要知道，在现实应用中，一个数据集有上千万的属性(维度)是非常常见的。

因此，我们要对一组高维度数据进行分析，最好找出那些最具代表性的维度，来减少我们要分析的维度。请注意，我们不是选出，而是找出最具代表性的维度。

还是拿淘宝店的例子来说，下单数和成交数是不同的概念，虽然两者很接近，但是细微的差别还是显示了这家店的特征，比如说，如果下单数比成交数高了100单，那么就说明这家店的货可能有问题，有100个人退货。所以，单纯去掉其中的一个维度，选择另一个，是会出问题的。那么，我们是不是可以创造一个维度，这个维度即显示了下单数的特征，又显示了成交数的特征呢？我们说”找出维度”，其实就是这个意思。

1.2 简单实例

现在，我们有这么一组二维数据 (虽然二维数据没必要做降维，但是超过三维的数据画不出来，所以以二维数据为例)。

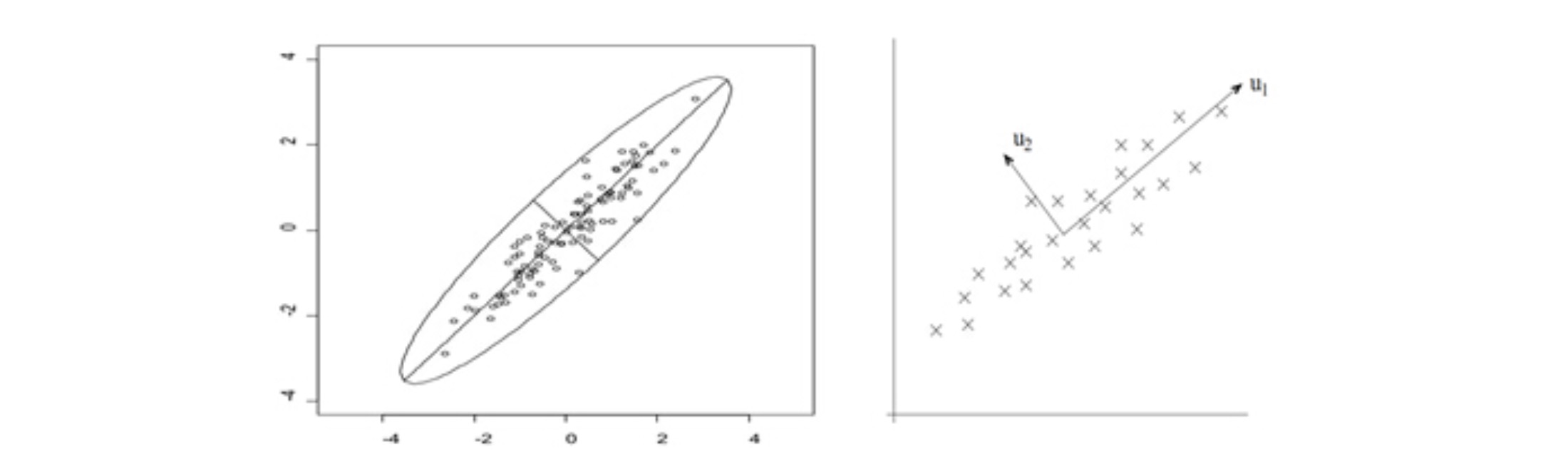
这组二维数据的维度可以由横坐标和纵坐标所代表，因此每个观测值都有相应于这两个坐标轴的两个坐标值。

我们看到，这些数据形成一个椭圆形状的点阵，这个椭圆有一个长轴和一个短轴。在短轴方向上，数据变化很少。短轴上的数据都差不多集中在一个部分，说明每一个数据在这个方向上的变化不大。所以，即使我们把这个椭圆沿着短轴方向往里压，压成一条直线，还是能很好地表示这组数据的变化趋势。这样，由二维到一维的降维就自然完成了。

这个长轴的方向叫做主成分方向，n个数据在主成分方向的离散程度最大，数据在主成分方向上的投影代表了原始数据的绝大部分信息，即使不考虑短轴，信息损失也不多。

我们可以看到，椭圆的长短轴相差得越大，损失的信息就越少。

问题是，我们怎么找到这个主成分方向呢？

2 矩阵乘法的本质——基变换(向量缩放)

找到主成分方向是我们最终的目标，我们需要对这个问题进行分析、细化、分解，从而可以将这个问题形式化为数学问题。在进行分析之前，我们首先得回顾一下线性代数的知识。我们回顾线性代数的知识，是为了解决一个问题：怎么把这个椭圆沿着短轴方向往里压，压成一条直线呢？这就涉及到线性变换的问题。

这里直接给出结论：矩阵乘法的实质，就是线性变换。把这些数据压成一条直线，实际上就是把这些数据进行一个特定的拉伸缩放，数学化就是乘上一个特定的矩阵。下面进行简单的阐述。

向量实际上是由基向量组成的，任何向量都可以分解成基向量的线性组合，我们一般都默认基向量$\vec{i}=(1,0)$，$\vec{j}=(0,1)$，向量$A=(3,2)$，其实是$A=3\vec{i}+2\vec{j}$，如图

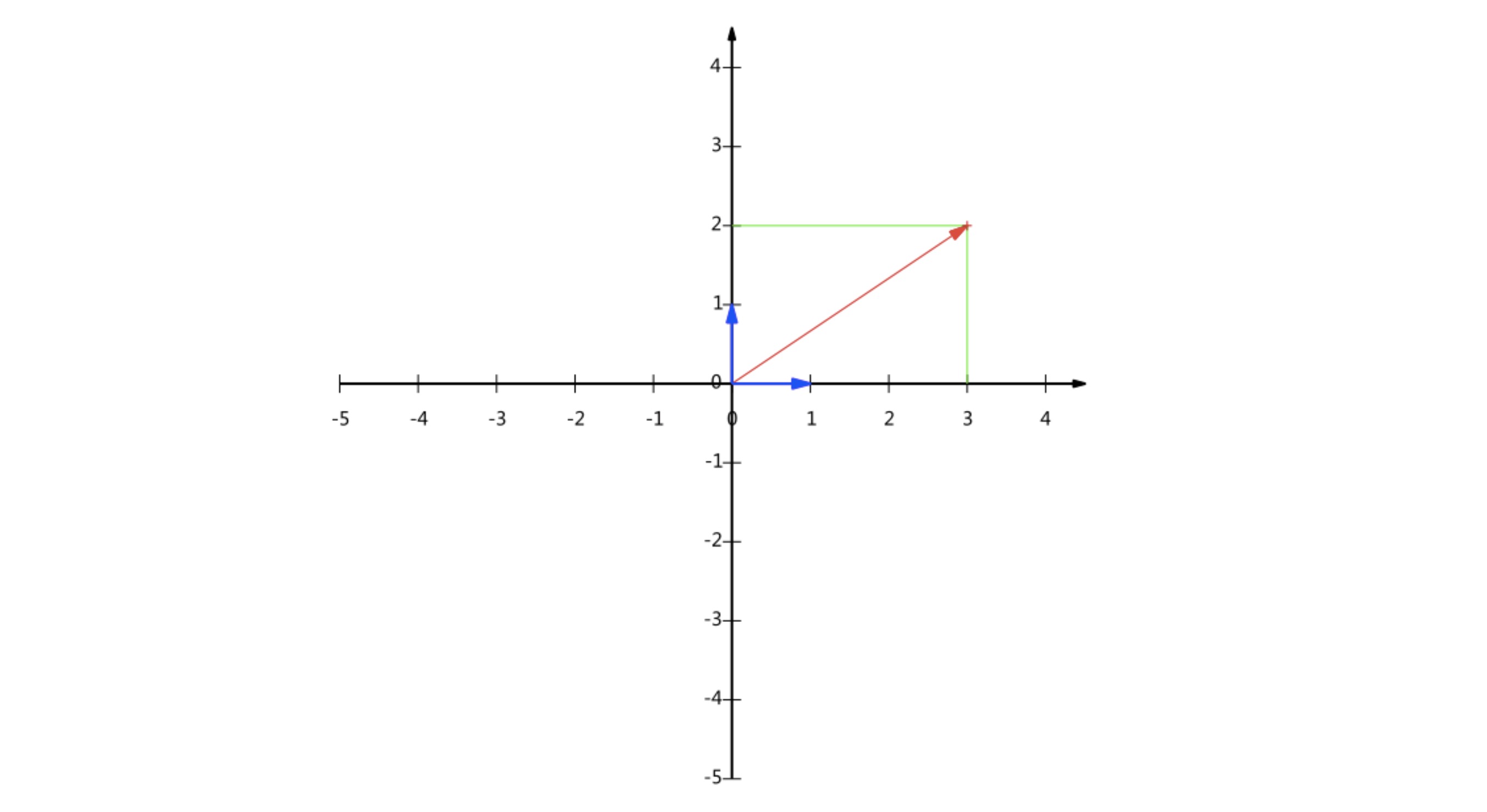
但是，其实只要线性无关，任何一对向量都可以成为一组基，如图就是另一组基。

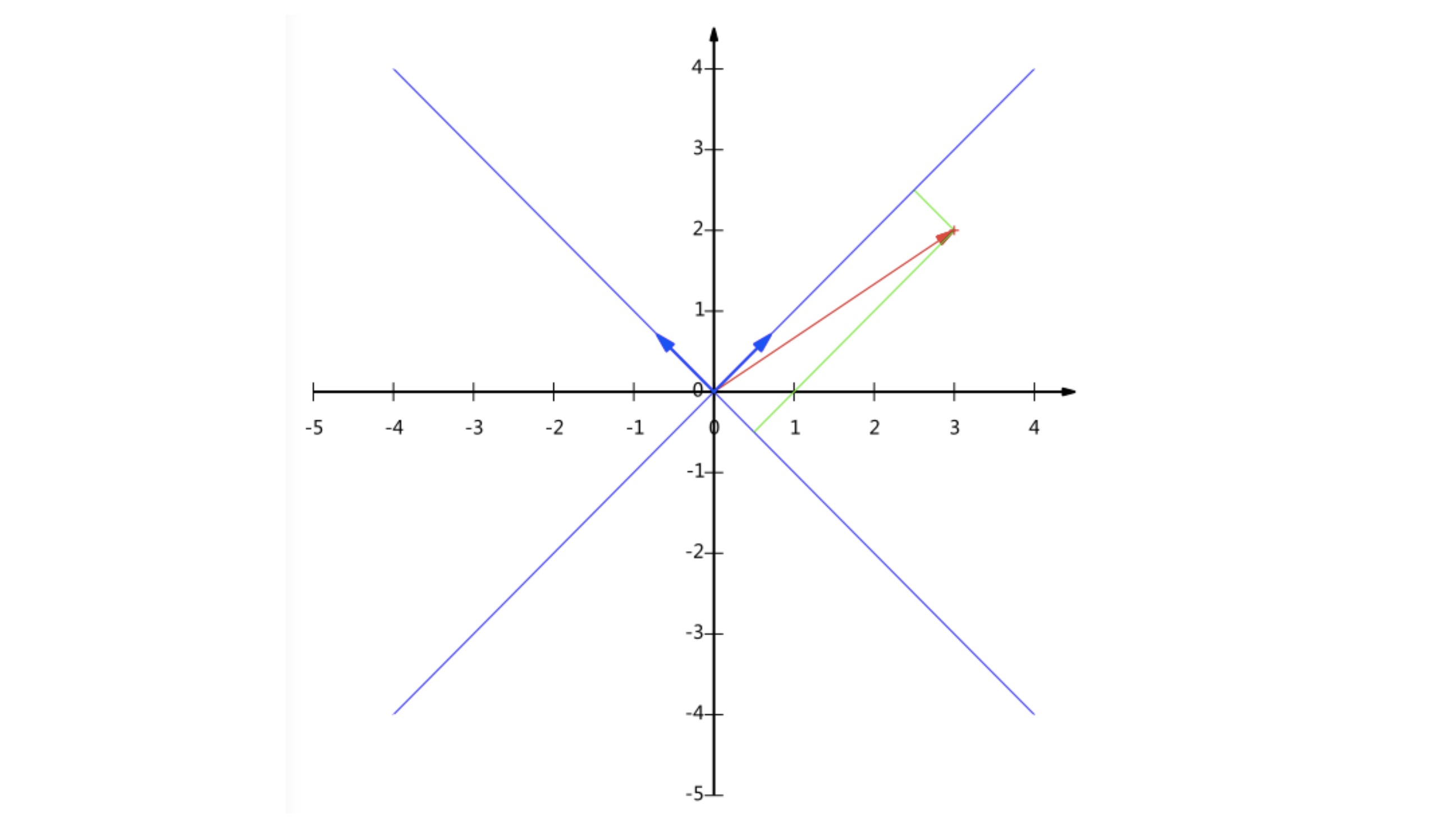
线性变换是什么？

线性变换实际上是对整个空间的拉伸缩放，而向量的变换只是整个空间变换的体现。我认为，我们的宇宙由一组规则组成，万物从一片寂静构成这个世界，都只是在依照这一组规则。这个想法套用在线性代数里，可以这么想：整个线性空间是由一组基构成的，线性空间实际上是基的另一种表现形式。那么，所谓线性空间的变换，实际上就是基的变换。

之前我们说过，向量实际上是由基向量组成的，任何向量都可以分解成基向量的线性组合，向量$A=(3,2)$可以表示为：

$$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix}$$

我们看到，就是基向量与$(3,2)$的内积运算。可以这样理解：$(3,2)$是某个绝对标尺，表示对某个事物属性的绝对表示，这个表示不受任何外部因素的影响。而为了把这个标尺表现在一个线性空间中，我们需要对这个标尺做一个变换，使得这个标尺能够合理地出现在这个线性空间里，而这个变换，就是与基向量的内积。

下面是一个形象的例子，描述了$(-1,2)$在基向量$(3,1),(1,2)$作用下的变换：

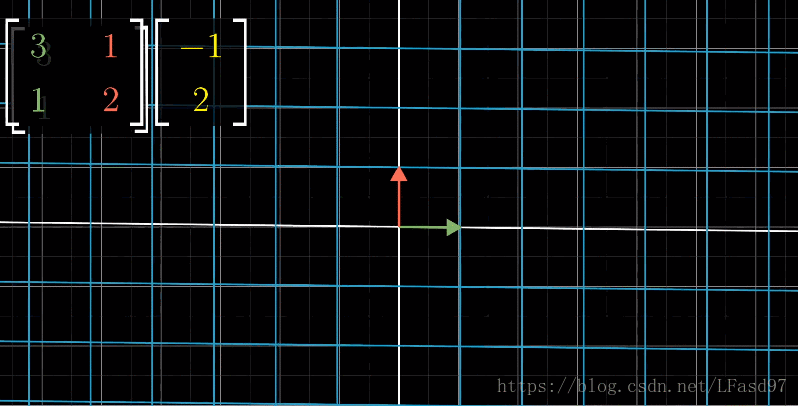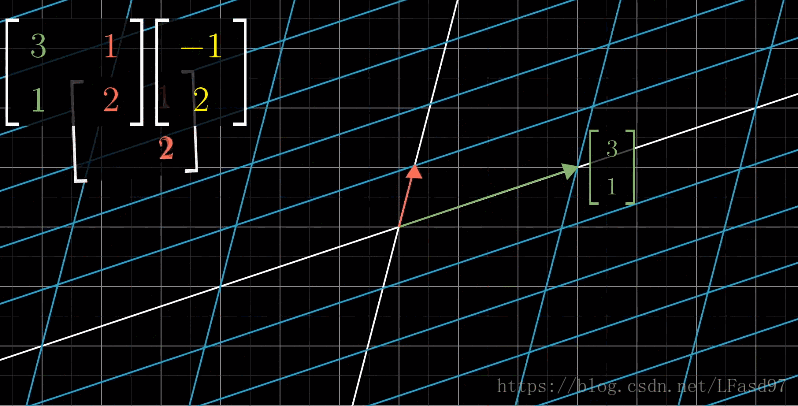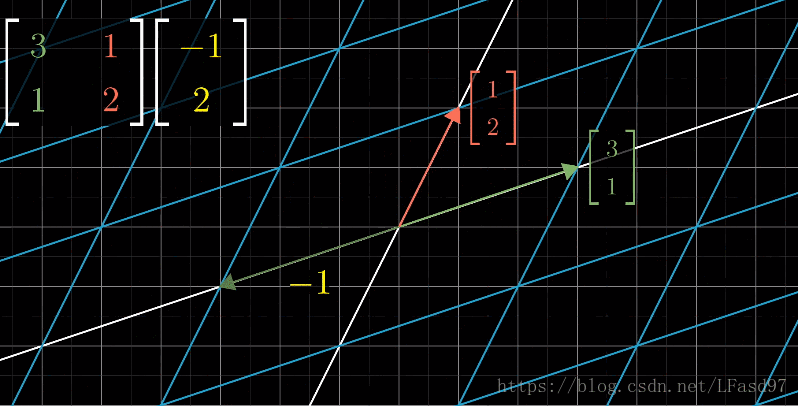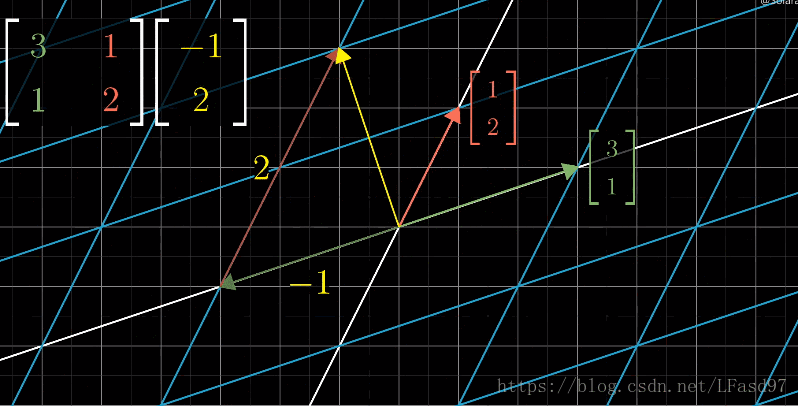
如果我们把$\vec{i}=(1,0)，$$\vec{j}=(0,1)$这个基向量逆时针旋转45°，那么此时，$\vec{i}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\vec{j}=(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$就作为了基向量，此时$(3,2)$在哪儿了呢？我们只要仍然把基向量与$(3,2)$相乘，就可以了:

$$\begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \\ -1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 5/\sqrt{2} \\ -1/\sqrt{2} \end{pmatrix}$$

可以画出来看看，这个结果确实是$(3,2)$旋转45°的结果。

所以，我们可以看到，矩阵乘法的实质，就是线性变换。详细的内容，可以转到线性代数的本质 - 03 - 矩阵与线性变换(“线性代数的本质”系列非常非常棒，强烈推荐看一遍)。

这和我们的降维有什么关系呢？接着看。

假设我有三个值，$(1,1)，(2,2)，(3,3)$，组成一个数据矩阵，行代表维度，列代表样本数，这里表示二维三个样本。

$$\left( \begin{array}{lll}{1} & {2} & {3} \\ {1} & {2} & {3}\end{array}\right)$$

这三个值在$y=x$这条直线上，所以这条直线就是我们的主成分方向。我们的目标就是把我们的二维空间$X,Y$变换到一维空间里，这个一维空间就是$y=x$这条直线。我们就这样表示：

$$\left( \begin{array}{cc}{1 / \sqrt{2}} & {1 / \sqrt{2}} \\ {-1 / \sqrt{2}} & {1 / \sqrt{2}}\end{array}\right) \left( \begin{array}{ccc}{1} & {2} & {3} \\ {1} & {2} & {3}\end{array}\right)=\left( \begin{array}{ccc}{2 / \sqrt{2}} & {4 / \sqrt{2}} & {6 / \sqrt{2}} \\ {0} & {0} & {0}\end{array}\right)$$

因为第二行都是0，无意义，所以我们把第二行去掉，原本的二维数据就变成了一个一维的数据。

3 方差

我们在上文说，我们要找到一个方向，在这个方向上，数据散得最大，而分散程度，可以用方差来表示。一个维度的方差是：

$$Var(a)=\frac{1}{m}\sum_{i=1}^m{(a_i-\mu)^2}$$

其中，$a$是一个维度，$a_i$是指这个维度下的第i个数据值，$\mu$是指这个维度下所有数据值的平均值。

于是上面的问题被形式化表述为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

4 协方差

对于上面二维降成一维的问题来说，找到那个使得方差最大的方向就可以了。不过对于更高维，我们没办法只考虑使得方差最大，比如说我要把考虑三维降到二维，我要找到两个主成分方向，这时候几乎不可能同时最大化两个方差。

所以我们换一种思路，从直观上说，让两个维度尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个维度不是完全独立，必然存在重复表示的信息。所以，我们要做的是，找出两个相关性为0的维度。

数学上，可以用协方差来表示两个属性的相关性，两个属性$a$, $b$的协方差为：

$$Cov(a,b)=\frac{1}{m}\sum_{i=1}^m(a_i-\mu_a)(b_i-\mu_b)$$

协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵)。

例如，对于2维数据(x,y)，计算它的协方差就是：

$$\operatorname{Cov}(X, Y)=\left[ \begin{array}{ll}{\operatorname{Cov}(x, x)} & {\operatorname{Cov}(x, y)} \\ {\operatorname{Cov}(y, x)} & {\operatorname{Cov}(y, y)} \end{array}\right]$$

我们可以看到，协方差矩阵的主对角线就是x、y的方差，方差与协方差被统一在一个协方差矩阵里了。

所以，我们寻找主成分方向的问题，变成了下面这个问题：将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。

这时候，我们来做一个神奇的操作，我们把每一个维度的每一个数值都减去这个维度的均值(期望)。这样之后，每一个维度的期望都是0，那么协方差就变成了：

$$\operatorname{Cov}(a, b)=\frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i}$$

协方差矩阵就是：

$$\left( \begin{array}{cc}{\frac{1}{m} \sum_{i=1}^{m} a_{i}^{2}} & {\frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i}} \\ {\frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i}} & {\frac{1}{m} \sum_{i=1}^{m} b_{i}^{2}}\end{array}\right)$$

我们把a、b两个维度的数据放在一个，形成一个数据矩阵X：

$$X=\left( \begin{array}{llll}{a_{1}} & {a_{2}} & {\cdots} & {a_{m}} \\ {b_{1}} & {b_{2}} & {\cdots} & {b_{m}}\end{array}\right)$$

最神奇的事情发生了，我们就会发现，协方差矩阵实际上就等于数据矩阵的内积：

$$\frac{1}{m} X X^{\top}=\left( \begin{array}{cc}{\frac{1}{m} \sum_{i=1}^{m} a_{i}^{2}} & {\frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i}} \\ {\frac{1}{m} \sum_{i=1}^{m} a_{i} b_{i}} & {\frac{1}{m} \sum_{i=1}^{m} b_{i}^{2}}\end{array}\right)$$

4.1 协方差矩阵对角化

我们接下来要做的，就是把除主对角线以外的元素化为0，并且将对角线上的元素从大到小排列，选择几个方差最大的元素，作为我们的主成分方向。

由第2部分的基变换，我们知道，找出主成分方向，实际上就是把数据所在的空间进行伸缩扭曲，也就是一个矩阵乘法。所以，我们的目的其实是找出一个$P$，使得$Y=PX$的协方差除对角线外的元素都是0。那么怎么求$P$呢？我们来推导一下。

假设$Y$的协方差矩阵是$D$，$X$的协方差矩阵是$C$，那么：

$$\begin{array}{l l l} D & = &\frac{1}{m}YY^\mathsf{T} \\ &= &\frac{1}{m}(PX)(PX)^\mathsf{T} \\ & = &\frac{1}{m}PXX^\mathsf{T}P^\mathsf{T} \\ & = &P(\frac{1}{m}XX^\mathsf{T})P^\mathsf{T} \\ &= &PCP^\mathsf{T} \\ \end{array}$$

这是不是很熟悉？看看特征向量与特征值的定义：

设A是n阶矩阵，如果数λ和n维非零向量x使关系式$A x=\lambda x$成立，那么，这样的数λ称为矩阵A的特征值，非零向量x称为A的对应于特征值λ的特征向量。

我们把这个式子挪一挪，则有：

$$\lambda=x^\mathsf{T}Ax$$

由上文知道，协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1）实对称矩阵不同特征值对应的特征向量必然正交。

2）设特征向量$\lambda$重数为r，则必然存在r个线性无关的特征向量对应于$\lambda$，因此可以将这r个特征向量单位正交化。

由上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为$e_1,e_2,⋯,e_n$我们将其按列组成矩阵：

$$E=(e_1\ e_2\ …e_n)$$

则对协方差矩阵C有如下结论：

$$E^\mathsf{T}CE=\Lambda=\begin{pmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{pmatrix}$$

其中，$\Lambda$的对角元素就是各特征向量对应的特征值。

到这里，我们发现我们已经找到了需要的矩阵P：

$$P=E^\mathsf{T}$$

P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。$\Lambda$则是将除对角线以外所有元素化为0后的结果。如果设P按照$\Lambda$中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

算法步骤总结

设有$m$条$n$维数据。

1）将原始数据按列组成$n$行$m$列矩阵$X$

2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵$C=\frac{1}{m}XX^\mathsf{T}$

4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前$k$行组成矩阵$P$

6）$Y=PX$即为降维到$k$维后的数据

Reference

PCA的数学原理(这篇博文非常棒，简单易懂地介绍了PCA”是什么”（算法思想）、”从哪儿来”（算法基础）、”到哪儿去”（目的）的问题。)

主成分分析（PCA）原理详解

线性代数的本质 - 03 - 矩阵与线性变换