本文是对如下公式的理解：

1 基础思想

用机器学习做分类，机器学习方法本质上是：

1. 将原点映射到一个高维或者低维空间，以便于使得原本线性不可分的数据，在映射后变得线性可分。这个映射的过程，是通过函数 $h_{\theta}()$实现的，更具体的，是通过函数中的参数$W$来实现的。
2. 在将数据映射到另一个空间后，数据变得线性可分了，因此，我们就可以通过一个判断函数 $d()$ ，来判断数据点的类型，实现二分类。

我们可以看到，机器学习分类的本质，就是将线性不可分的数据变得线性可分（ $h_{\theta}()$ ），然后划一条线（ $d()$ ），实现分类。这个过程需要学习的只有一个变量：$W$。

而学习参数的过程，可以这样解释。我们为什么要学习参数？因为现在的参数效果不好。具体来说，什么叫效果不好？就是对映射后的数据进行分类，结果是错的。因此，我们可以很直观地看出，可以设置一个函数，来度量在某一个参数$W$下的性能，这个函数的结果是一个成绩，展现的是这个参数的效果有多差，成绩越低，说明参数越好，这个函数的名字叫“代价函数”。

只要能度量参数好不好，都叫代价函数。我们提供一种方式，是线性回归的代价函数：

$$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \frac{1}{2}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$$
我们看到，这个式子实际上是一个二范式，度量了映射后的值$h_{\theta}(x^{(i)})$和真实值$y^{(i)}$的距离，这个距离，相当于相似度。而前面的$1/m$，可以理解为，每一个数据$x^{(i)}$和真实值的距离之前的距离，地位都是相等的。

2 自适应近邻学习法

我们使用相似度矩阵（Similarity Matrix）来度量不同样本间的相似度。计算相似度矩阵，一般来说相似度矩阵是在数据进行映射之前做的，但是有一个问题是，当数据的维度发生变化，样本间的相似度也可能发生不同程度的变化。我们知道，降维实际上是揭示了数据更进一步的特征、本质，所以实际上高维数据的相似度矩阵不能很好刻画降维后的数据之间的相似度。因此，我们提出了自适应近邻学习方法（Similarity Learning）。

就如我们上面讨论过的，我们需要一个损失函数，来表示参数的好坏，这里也一样，我们定下一个损失函数如下：
$$
\begin{array}{c}{\min _{s_{i}} \sum_{j}^{n}\left|x_{i}-x_{j}\right|{2}^{2} s{i j}} \ {\text { s.t. } \sum_{j}^{n} s_{i j}=1} \ {0 \leq s_{i j} \leq 1}\end{array}
$$
为什么这么定呢？因为直观来看，如果样本$x_i$和$x_j$之间具有较小的距离$d_{ij}= |x_i-x_j|^2$，那么$x_j$就有较大的概率$s_{ij}$和$x_i$成为近邻。

$\sum_{j}^{n}|x_{i}-x_{j}|{2}^{2} s{i j}$表示的是一个损失，如果两个样本之间有较小的距离，那么他们的概率就会变大，也就是说这个较小的距离所占整个结果的比重就更大，如果有较大的距离，那么概率变小，所占结果的比重就更小。因此，当我们最小化这个式子，直观上理解，就是求得一连串的概率，使得其能够完美满足这个直觉：如果样本$x_i$和$x_j$之间具有较小的距离$d_{ij}= |x_i-x_j|^2$，那么$x_j$就有较大的概率$s_{ij}$和$x_i$成为近邻。

但是实际上存在一个平凡解，就是最小距离的那两个样本的概率为1，其他都为0。为了避免这种情况，我们加入一个正则项 $\gamma s_{ij}^2$，使得平凡解消失。
$$
\begin{array}{c}{\min _{s_{i}} \sum_{j}^{n}\left(\left|x_{i}-x_{j}\right|{2}^{2} s{i j}+\gamma s_{i j}^{2}\right)} \ {\text { s.t } \sum_{j}^{n} s_{i j}=1} \ {0 \leq s_{i j} \leq 1}\end{array}
$$
􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱼􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱼􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱼􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏰵􏱼􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻􏳼􏰮􏲷􏰳􏰴􏱵􏱶􏰕􏰖􏲊􏴴􏰷􏲇􏱈􏰍􏱨􏱠􏱩􏴵􏱪􏱃􏱪􏰖􏰍􏱾􏱷􏱿􏰾􏳻

3 多模态特征选择

先上公式：
$$
\min {W, S} \sum{m}^{M} \sum_{i}^{N}\left|y_{i}-\boldsymbol{w}{m}^{T} \boldsymbol{x}{i}^{m}\right|{2}^{2}+\lambda|\boldsymbol{W}|{2,1}
$$
假设有$M$个模态数据，其中第$m$个模态的数据矩阵为$\boldsymbol{X}^{m}=\left[\boldsymbol{x}{1}^{m}, \boldsymbol{x}{2}^{m}, \ldots, \boldsymbol{x}{N}^{m}\right]^{T} \in \mathbb{R}^{N \times d{m}}$，$N$为样本总数，$d_m$为相应的模态数据维度。$\boldsymbol{W}=\left[\boldsymbol{w}{1}, \boldsymbol{w}{2}, \ldots, \boldsymbol{w}{M}\right] \in \mathbb{R}^{d \times M}$为回归系数，而$\lambda|\boldsymbol{W}|{2,1}$的目的是为了能够对矩阵$W$起到行稀疏的作用，$W$就用做特征选择。

行稀疏：只有每一行的L2范数都最小，才能达到约束问题最小化。而每一行的L2范数取得最小的含义是，当行内尽可能多的元素为0（甚至为全零行）时，约束才可能取得最小。这就实现了行稀疏（使得矩阵出现尽可能多的全零行）。

回到我们第一部分所讲的机器学习的本质，我们解释说，首先我们需要将原点映射到一个高维或者低维空间，以便于使得原本线性不可分的数据，在映射后变得线性可分。这个映射的过程，是通过函数 $h_{\theta}()$实现的，更具体的，是通过函数中的参数$W$来实现的。而在这里，我们把$W$解释为，特征选择。直观上理解为，使得数据在经过特征选择之后，与其原本的标签更相似。

回头想想，将数据映射到低维，也可以理解为特征选择。我们之前提到$W$起的作用是降维，但实际上降维本来就是特征选择的结果啊。

OK我们拉回来。上面这个公式也是一个损失函数，用来选择更好的$W$，来实现更完美的数据降维。

4 自适应近邻多模态特征选择

我们在第二部分讲过，当数据的维度发生变化，样本间的相似度也可能发生不同程度的变化。我们知道，降维实际上是揭示了数据更进一步的特征、本质，所以实际上高维数据的相似度矩阵不能很好刻画降维后的数据之间的相似度。

但是，我们也不能完全确定降维过后的结果真的准确刻画了数据的本质特性，所以，我们可不可以让『降维』和『相似度』来相互约束，使得两者都达到最好的结果呢？

我们把两个部分的式子结合起来看看：

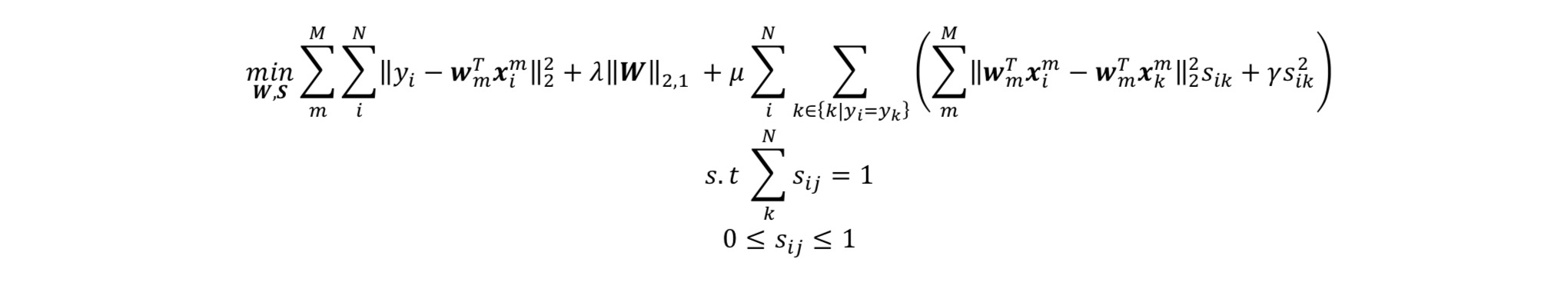
针对这个式子的后半部分，我需要提一句，这个实际上，就是PCA的目标公式。具体解释如下：

PCA的目标是寻找$W$，使得投影过后的数据有最大的方差或最小重建误差：

$$\boldsymbol{w}=\underset{\boldsymbol{w}^{T} \boldsymbol{w}=1}{\operatorname{argmin}} \boldsymbol{w}^{T} \boldsymbol{C w}$$
其中$\boldsymbol{C}=1 / N \sum_{i}^{N}\left(\boldsymbol{x}{i}-\overline{\boldsymbol{x}}\right)\left(\boldsymbol{x}{i}-\overline{\boldsymbol{x}}\right)^{T}$。那么我们将$1/N$定义为$s_{ij}$，上面的公式就变成了：$$
\boldsymbol{w}=\underset{\boldsymbol{w}^{T} \boldsymbol{w}=1}{\operatorname{argmin}} \sum_{i, j}\left(\boldsymbol{w}^{T} \boldsymbol{x}{i}-\boldsymbol{w}^{T} \boldsymbol{x}{j}\right)^{2} s_{i j}
$$
可以这样理解，$1/N=s_{ij}$意味着，对于PCA来说，每一个样本之间的相似性都是一样的，每一个样本都是彼此的近邻。

所以我们看到了，当固定$s_{ij}$的时候，我们实际上是在用PCA做一个降维问题，求的是$W$。当固定$W$的时候，我们实际上是在做一个自适应近邻学习，求的是$s_{ij}$。这两个参数就这样相互约束，相互学习，使得两者都达到了对彼此来说的最佳。