本文简单记录了我在学习Flow-based Model时的笔记，阐述了对模型概念、思路的模糊且不准确的理解。

昨天（11.4）在看ICCV2019的时候，看到一篇使用flow-based generative model来实现虚拟试穿的paper，作者提出了一个模型，只要把你的全身照和衣服的照片丢进模型里，就能生成一张你穿着这件衣服的图像，这个虚拟试穿功能犹如一道惊雷在电商时代炸开。对于我身边很多人来说，之所以还会去线下买衣服，只是因为能够试穿看看效果、试试尺码。但是除了功能上的创新，这篇paper最吸引我的是flow-based generative model，一个我之前从来没有听说过的生成模型。

GAN是目前最火爆的生成模型，基本上每个顶会都有好多篇做GAN的。因为最近我和GAN在一起的时间比较长，对GAN的特性有一个大概、模糊的全局观。日久生情，而又爱屋及乌，这次看到除了GAN、autoencoder之外的生成模型，就很好奇，也很期待。flow到底是什么呢？一查，嚯，不得了，“超越GAN的生成模型”。

熬夜学习了flow的基本知识，也对flow的想法、技巧有了粗略的掌握。这次打算写一篇马马虎虎的学习笔记，主要记录一些思路上、概念上的想法，具体的推算就pass了。毕竟概念和思路最重要，零零碎碎的东西，花时间就能学了。

基本概念

大家都可以理解，一个事物之所以区别于另一个事物，是因为这个事物具有自己的特征，所以对于属于同一类事物的个体们来说，他们虽然各不相同，有的人耳朵大，有的人眼睛小，但是在“人”这个维度上说，都是一模一样的。生成模型为了能够生成一张人脸图像，就得从一大堆（成千上万）的人脸图像中学习到人脸的特征：比如眼睛长什么样子，嘴巴在哪个位置。从统计学上讲，生成模型的本质目的是为了学习一个分布$q(x)$，使得$q(x)$逼近真实数据的分布$p(x)$。

基本步骤

任何复杂的事物都是有最简单的成分组成的，我有一个符合某一个分布（高斯分布等）的特征向量$z$，我就能通过复杂的映射过程$g:z \rightarrow x$，投影到一个复杂的空间中。我同样可以使用映射的逆过程，将复杂空间投影到简单空间中$f:x \rightarrow z$。其中$g=f^{-1}$。

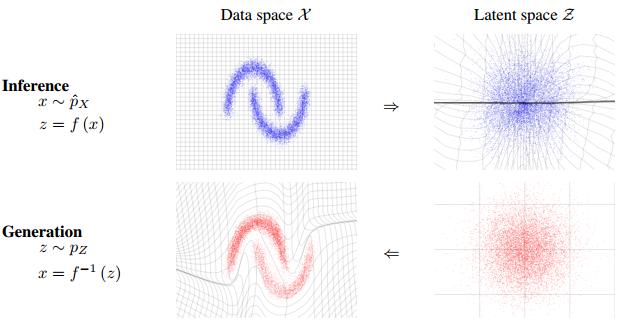
给定两组数据$z$和$x$，其中$z$服从已知的简单先验分布$π(z)$（通常是高斯分布），$x$服从复杂的分布$p(x)$（即训练数据代表的分布），现在我们想要找到一个变换函数$g$，它能建立一种$z$到$x$的映射$g:z\rightarrow x$，使得每对于$π(z)$中的一个采样点$z’$，都能在$p(x)$中有一个（新）样本点$x’$与之对应。

$\boldsymbol{x}=\boldsymbol{g}(\boldsymbol{z}) \Leftrightarrow \boldsymbol{z} = \boldsymbol{f}(\boldsymbol{x})\tag{3}$

如果这个变换函数能找到的话，那么我们就实现了一个生成模型的构造。因为，$p(x)$中的每一个样本点都代表一张具体的图片，如果我们希望机器画出新图片的话，只需要从$π(z)$中随机采样一个点，然后通过$g:z\rightarrow x$，得到新样本点$x$，也就是对应的生成的具体图片。

怎么评估分布$q(x)$与$p(x)$近似呢？直觉上说，因为所有那些真实数据组成了$p(x)$，所以在$p(x)$下，$N$个数据出现的可能性加起来就为1，即：
$$
\int_{-\infin}^{\infin} p(x)dx=1\tag{1}
$$
所以，我们要尽可能地使得使得每一个采样的$X_i$在经过这个分布后结果之和最大。数学一点，我们要最大化目标函数：
$$
\mathbb{E}_{\boldsymbol{x}\sim \tilde{p}(\boldsymbol{x})} \big[\log q(\boldsymbol{x})\big]\tag{2}
$$

GAN与VAE

GAN怎么去学习这个分布呢？它们没有去解这个目标函数，因为Goodfellow解不出来。GAN通过Discriminator和Generator来交替训练迭代，使得生成图像越来越像训练图像，既然生成的图像都像训练图像了，那么我们就可以认为$q(x)$越来越接近$p(x)$。我认为，GAN的学习是粗暴的模仿，它没有让$q(x)$变得接近$p(x)$，也就是说它没有去改变本质，而是通过优化生成图像这个外在表现，来拖着$q(x)$变得像$p(x)$。$q(z)$需要被生成图像拖着，在茫茫人海中慢慢靠近$p(z)$，靠近了自然好，但是这个靠近的过程很艰难，而且不准确（两者不能完全相等，只能做到相对近似）。

举个例子，考试的目的是检验同学掌握的情况。为什么不直接去测量同学掌握的情况呢？因为没办法直接去测量，所以只能通过分数，来反映同学掌握知识的情况。自然，一个同学分数越高，可以说他掌握了知识，但是毕竟他的目的是为了提高分数，而不是为了掌握知识，所以很可能出现，他成绩很高，但是其实啥都不知道（当然这种情况很少见）。

VAE的重要概念是变分推断。变分推断简单来说便是需要根据已有数据推断需要的分布$P$；当不$P$容易表达，不能直接求解时，可以尝试用变分推断的方法。即，寻找容易表达和求解的分布$Q$，当$Q$和的$P$差距很小的时候，$Q$就可以作为$P$的近似分布代替$P$。VAE怎么学习这个分布呢？衡量两个分布的相似程度的一种标准便是$KL$散度，$KL$的值越小表示两种分布越相似。什么时候最小呢？只要$KL$便是最小，这个条件看似说明了一切，但是我们只知道$Q$不知道$P$的分布啊，没法确定两者是否为0。通过变分推断（使得$ELBO$最大化的这种间接的方式）从而使得$KL$散度尽可能的小。它也没有优化目标函数，同样用了一种暴力的方法：通过计算$KL$散度来近似计算两个分布的距离，但由于无法确知目标分布的特性，实际上只能依靠mean和variance来计算两者之间的分布差异性的下限。所以VAE只能近似，而不能完全相似，因此生成图像的质量不高。

之前VAE的支持者酸酸地说，虽然我们VAE生成的图像烂，但是人家能encoder图像，输出一个图像的隐空间特征，相当于发现了图像的内在表征，我们就可以试图通过改变表征来控制生成图像的内容，而GAN就只是生成图像的傻大个，控制不了生成的内容。但是BiGAN的提出彻底把VAE的最后一个优点打破了：BiGAN加入了encoder模块，GAN也能学习图像内在表征了。

Flow

VAE和GAN的能力强，但都是死记硬背。GAN通过博弈，让$q(x)$无限逼近$p(x)$，但是非常不优雅。VAE则通过优化$KL$散度上界来训练$q(x)$慢慢靠近$p(x)$。

Flow可以说既直接，又委婉。说flow直接，是因为它从本质入手，直接去解目标函数(2)，而不是像GAN一样拐弯抹角地要通过生成图像来优化。说flow委婉，是因为这个目标函数是解不出来的，但是它用了非常秒的trick，把这个目标函数改得可解了。

一种不同于 VAE 和 GAN 的生成模型——flow 模型徐徐揭开了面纱，它通过巧妙的构造，让我们能直接去拟合概率分布本身。

我们通常将$q(z)$作为一个高斯分布：
$$
q(\boldsymbol{z}) = \frac{1}{(2\pi)^{D/2}}\exp\left(-\frac{1}{2} \Vert \boldsymbol{z}\Vert^2\right)\ \tag{3}
$$
因为$x$到$z$的映射为$f:x \rightarrow z$，所以上式可以变为：
$$
q(\boldsymbol{x}) = \frac{1}{(2\pi)^{D/2}}\exp\left(-\frac{1}{2}\big\Vert \boldsymbol{f}(\boldsymbol{x})\big\Vert^2\right)\left|\det\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right]\right|\\tag{4}
$$
看到这里多出了一个行列式$|\det[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}]|$，这个行列式叫雅克比行列式（Jacobian），在n维欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响，而 Jacobian 也是如此，它描绘了一个比例关系：对于非线性映射来说，但其微元变换实际上可以看做是线性的，因此雅可比行列式实际意义就是坐标系变换后单位微元的比率或倍数。

进一步变换式 (4)：
$$
\log q(\boldsymbol{x}) = -\frac{D}{2}\log (2\pi) -\frac{1}{2}\big\Vert \boldsymbol{f}(\boldsymbol{x})\big\Vert^2 + \log \left|\det\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right]\right|\tag{5}
$$
我们的目的就是求出$f(x)$，最大化下式：
$$
\mathbb{E}{\boldsymbol{x}\sim \tilde{p}(\boldsymbol{x})} \big[-\log q(\boldsymbol{x})\big] = \mathbb{E}{\boldsymbol{x}\sim \tilde{p}(\boldsymbol{x})} \big[\frac{D}{2}\log (2\pi) +\frac{1}{2}\big\Vert \boldsymbol{f}(\boldsymbol{x})\big\Vert^2 - \log \left|\det\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right]\right|\tag{5}\big]
$$
乍一眼看，这就是一个很简单的优化问题，用反向传播算法优化神经网络就可以了。但是仔细一瞧，最右边多了一项：$\log |\det[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}]|$ ，没那么简单，这个优化有两个要求

1. Jacobian容易计算；
2. $f(x)$可逆，且容易计算。

两个要求，都提出了一个问题：如何设计$f(x)$？

这就是Flow的厉害之处，也是它的核心。为了满足上述要求，Flow-based Model采用了一种称为耦合层（Coupling Layer）的设计来实现，它将$D$维的$x$分为两个部分$x_1$和$x_2$，并取以下变换：
$$
z_1=x_1
$$

$$
z_2=F(x_1) \odot x_2+H(x_1)
$$

计算过程如下图：

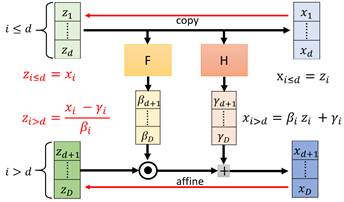
这样一来，Jacobian非常好算：

$$
\left[\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}\right]=\begin{pmatrix}\mathbb{I}_d & \mathbb{O} \ \left[\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{x}_1}\otimes \boldsymbol{x}_2+\frac{\partial \boldsymbol{H}}{\partial \boldsymbol{x}_1}\right] & \boldsymbol{F}\end{pmatrix}\tag{2}
$$

因为右上角是0，所以不管左下角是什么都无所谓，Jacobian的结果只是对角线上的行列式，也就是$F$各个元素之积。所以直接用一层神经网络建模输出$F$就好了。

然后很自然地会想到，为了增加$f(x)$非线性拟合能力，我们多加几层映射：

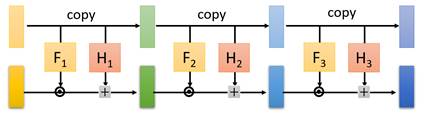
这样一个多耦合层结构，就是最终的$f(x)$。

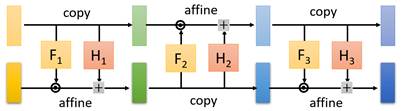
还有一个小问题，如果$x_1$一直copy下去，到最后剩的还是$x_1$，这不就是一团噪声嘛。所以可以通过交替复制模块（copy）与仿射模块（affine）来进行。如下图：

赏

谢谢你请我吃糖果

支付宝

微信